
Die Ping-Pong-Platine von ELO bietet nicht nur eine (Retro-)Spielplattform, sondern auch eine Entwicklungsumgebung, womit sehr unterschiedliche Anwendungsbereiche getestet werden können. Eine weitere Idee möchte ich hier gerne vorstellen. Der Atmega8-Mikrocontroller hat einen A/D-Wandler (ADC = Analog-to-Digital-Converter), der von der Firmware im Ping-Pong-Spiel zur Ablesung der Potentiometerstellungen und der entsprechenden Steuerung der Tischtennisschläger verwendet wird. Zudem eignet sich die Platine mit ihrer 12x10 LED-Matrix gut zur einfachen, grafischen Darstellung von Messwerten. Die beiden Ausprägungen der Platine -- vorhandener A/D Wandler und 120 frei ansteuerbare LEDs -- haben mich zur Idee der "Visualisierung" von Musik bzw. Audiosignalen angeregt. Jeder kennt das von Musikanlagen oder Computerprogrammen, die parallel zur Wiedergabe bunte Balken im Rhythmus der Musik anzeigen. Die Balken entsprechen dabei Stärke und Frequenz des Signals. Die Signalanalyse kann mit verschieden Mitteln durchgeführt werden. Ein Weg ist die "Diskrete Fourier-Transformation". Die komplexe, mathematische Transformation wird hier mittels eines schnellen Algorithmus "FFT" (Fast Fourier Transform / Schnelle Fourier-Transformation) durchgeführt. Die FFT liefert als Ergebnis die im abgetasteten Signal hauptsächlich vorkommenden Frequenzen mit den zugehörigen Amplituden, die als „bunte Balken“ auf dem Ping-Pong-Display angezeigt werden.
An sich nutzt der FFT-Algorithmus Fließkomma-Arithmetik (zur Berechnung der trigonometrischen Funktionen), was aber für den kleinen Atmega8 Mikrocontroller eine gewisse Herausforderung darstellt. Die Berechnung muss außerdem in Echtzeit erfolgen, damit der Rhythmus der Musik verfolgt werden kann. Für den „armen“ Atemag8 ist das definitiv zu viel. Aufgrund der verhältnismäßig "einfachen", grafischen Darstellung, kann auf die "höchste" Genauigkeit verzichtet werden und die "einfachere" Festkomma-Arithmetik verwendet werden.

Zudem können die trigonometrischen Werte "im voraus" bestimmt und in einer Tabelle als feste Werte gespeichert werden. Mit dieser Vorgehensweise läßt sich die FFT auch sehr gut in Assembler codieren. Um das Rad nicht neu zu erfinden, habe ich im Internet recherchiert und ich bin auf die Seite "http://elm-chan.org/works/akilcd/report_e.html" gestoßen, auf der eine fertige FFT-Lösung, freundlicherweise mit einem GPL-Lizenz-Model, vorgestellt wird. Diese Lösung hat als niedrigste Auflösung 32 Werte pro Analyselauf. Die Ping-Pong-Platine bietet aber nur 12 LED-Spalten. Deswegen muss das Ausgabeergebnis im Programm entsprechend angepasst werden. Das kann noch im Rahmen der FFT oder danach umgesetzt werden. Beide Fälle habe ich implementiert und getestet. Die Auflösung der FFT habe ich auf 16 Werte begrenzt (und dazu habe noch eine kleine Anpassung in der Datei ffft.S vorgenommen). Von den ursprünglich 32 Werten werden jeweils zwei benachbarte Frequenzwerte zusammengefasst und nur der größere der beiden angezeigt. Zudem werden sowohl die beiden niedrigsten als auch die beiden höchsten Frequenzen (plus Gleichstromkomponente) ausgelassen.
Mein Programm bietet darüber hinaus verschiedene Möglichkeiten der Darstellung. Die Balken können langsam runterfallen, schnell dem Signal folgen und nur einen maximalen Wert hinterlassen oder nur die maximalen Werte anzeigen. Zur Änderung der Darstellung nutze ich den vorhandenen Port D, Pin PD2 als Ansteuerung. Der Pin PD2 wird über einen Mikrotaster mit der Masse des Geräts verbunden. Deshalb bitte beachten, dass die Initialisierung des Ports und die Interrupt-Routine von mir leicht abgeändert wurden.
Als weitere Möglichkeit (der Darstellung) habe ich eine Art Oszilloskop implementiert. In diesem Modus kann die Zeitbasis mit dem linken Poti eingestellt werden. Allerdings sind hier Auflösung des Displays, die (niedrige) Abtastrate, sowie der Signaleingang für ein „professionelles" Oszilloskop nicht geeignet.
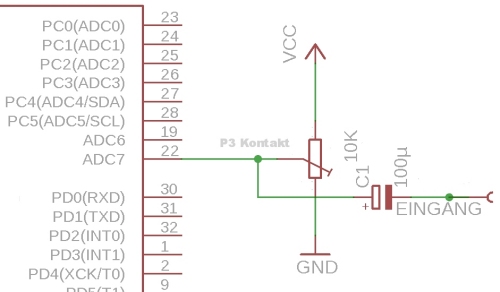
Auch wenn Anzeige und Genauigkeit der oben genannten Frequenzanalysedarstellung erstaunlich gut sind, sollte der Signaleingang hier noch einmal kurz besprochen werden. In der Grundversion wird das Audiosignal von der Kopfhörerbuchse direkt über einem Kondensator (100 µF) mit dem P3-Kontakt verbunden.

Wenn jemand einen „richtigen“ Audiofrequenzanalysator entwickeln möchte, sollte er den Signaleingang mit einem Tiefpassfilter (low-pass filter) versehen, um eine Glättung des Signals zu erreichen. Noch besser wäre ein Bandbreitenfilter, der für den vorgesehenen Audiofrequenzbereich ausgelegt (berechnet) ist. Als Beispiel möchte ich hier einen Bandbreitenfilter vorschlagen, der mit aktiven Elementen arbeitet (Operationsverstärker mit passiven Elementen versehen), der für eine Bandbreite von 20Hz-20kHz ausgelegt (berechnet) ist. Die zwei invertierenden Verstärker in Reihenschaltung sichern ein sauberes Ausgangssignal und eine gute Frequenzantwort.
Download: pong-fft-v2.zip