Analyse: Digitale Quellen gehen im Vergleich zu LPs sehr
beschränkt mit dem Frequenzspektrum um, das im Originalkonzert zu hören ist
und in solchem Sinne auch auf LPs geschnitten wurde.
Audioanalyse mit Audacity und Spectrum Lab, von Heinz D.
Durch die
Beschäftigung mit dem Lautsprecherbau ist mir das Thema Audacity nicht
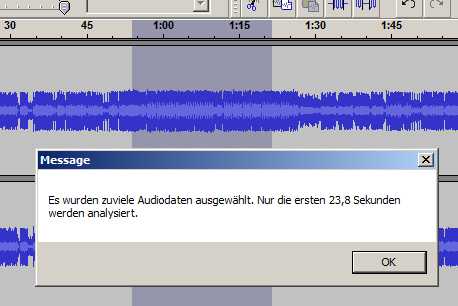
völlig unbekannt. Mein Audacity meldet mir, das es nur 23,8s
analysieren kann. Eine
Beurteilung des gesamten Files ist meines Erachtens somit schwer
möglich, weil man einen Abschnitt suchen muss, der alle typischen
Anteile enthält.
Zum Zweiten sind fast alle Messungen linear,
obwohl wir logarythmisch hören, sowohl beim Pegel, als auch bei der
Frequenz. Die Frequenz verdoppelt sich von Oktave zu Oktave. Eine
lineare Messung ist zur Beurteilung des Hörempfinden meines Erachtens
kaum geeignet. Im Bereich über 15kHz kann man zwar leicht Unterschiede
zwischen analogen und digitalen Aufnahmen aufzeigen (AD-DA-Wandler-,
Kompressor-Mängel, usw.), das hat nach meiner Erfahrung nur selten
Einfluss auf den Hörgenuss (hin und wieder schon).
Den Frequenzgang kann man, wie bei Lautsprechern, grob in drei Dekaden unterscheiden.
20-200Hz: Rythmus-Instumente,
200-2000Hz: Grundtöne der Stimmen und kleinerer Instrumente,
2k-20kHz: ausschliesslich ! pegelarme Obertöne, die den Charakter des Klangs ausmachen!
Die
erforderliche elektrische/akustische Leistung für ein
angenehmes/ausgewogenes Hören ist für 20-200Hz~90%, für 200-2000Hz~9%
und für 2k-20kHz nur 1% der Gesamtleistung. Auch hieran sieht man den
natürlichen Abfall zu höheren Frequenzen.
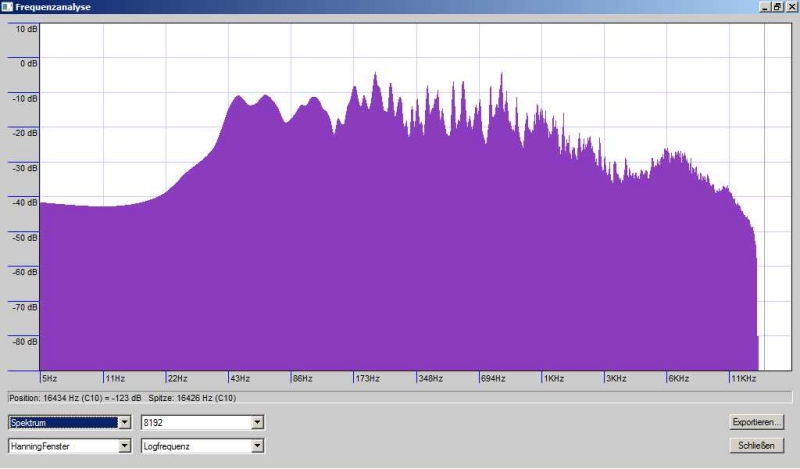
Im folgenden habe
ich zwei Stücke (die sicher nicht vom gleichen Toningeneur abgemischt
wurden) analysiert. Bei Audacity habe ich versucht einen typischen
Abschnitt zu finden. Die Begrenzung auf 16kHz kommt durch die
.mp3-Kompression. Mit Speclab wurden die Stücke ganz analysiert. Die
Ergebnisse beider Programm widersprechen einander nicht. Speclab ist
lediglich detailierter.
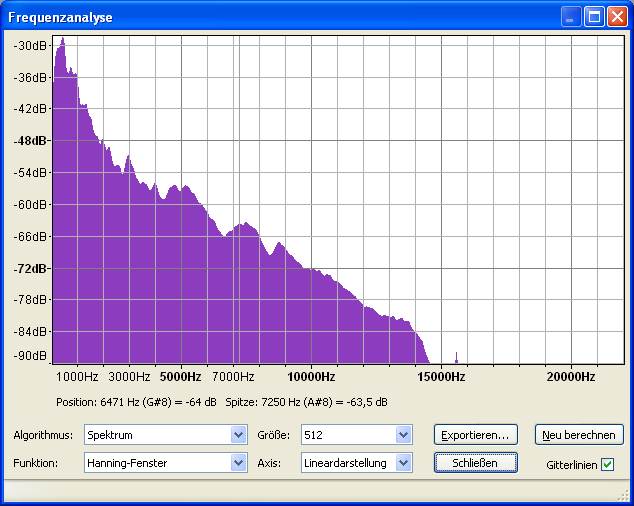
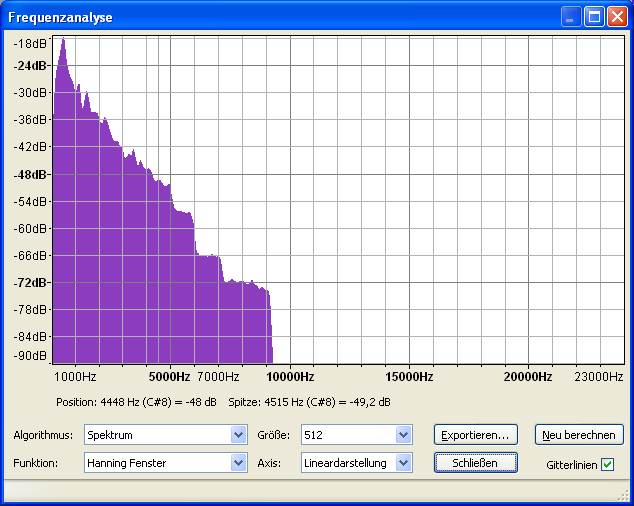
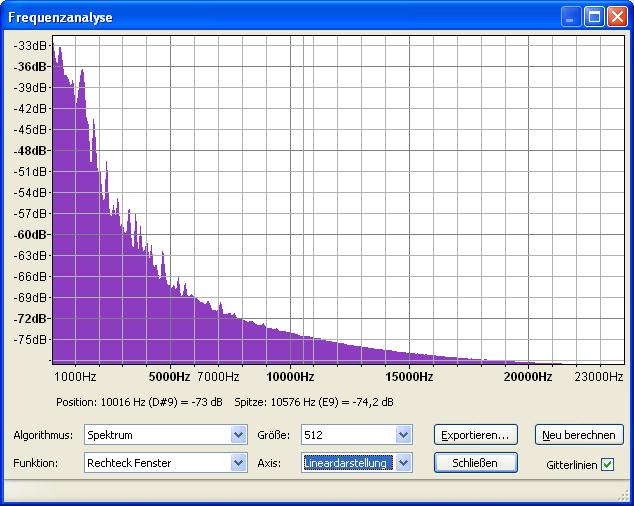
Bei Louis Armstrong (eine Art
Sprechgesang) ist seine Stimme bei ~200Hz gut zu erkennen. Trotz wenig
Bass und wenigen Obertönen kann man das Spektrum als ausgewogen
bezeichnen. Die geringere Helligkeit in Speclab bedeutet nur, das Louis
leiser als Tina ist.
Louis Armstrong
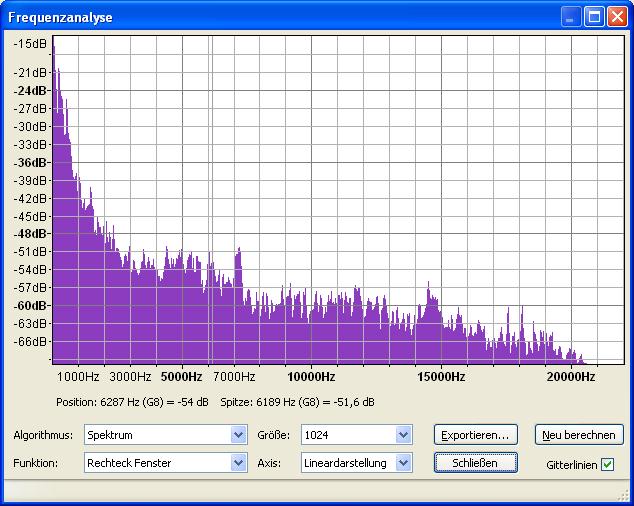
Bei
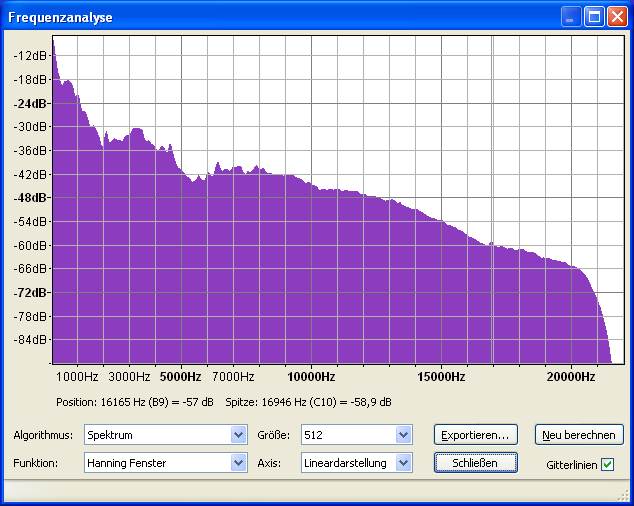
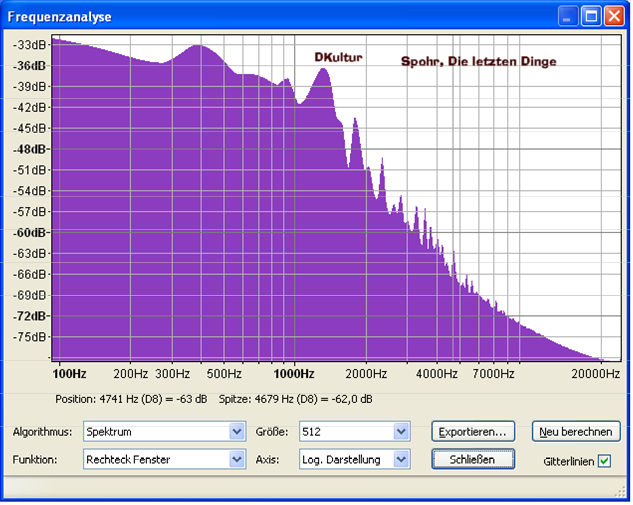
Tina Turner (Discomusik) fällt die Basslastigkeit auf. Die überwiegend
gelbe Farbe in Speclab zeigt jedoch auch, das die Pegelunterschiede
zwischen hohen und niedrigen Frequenzen nicht allzu hoch sind. Unser
Ohr kann bei einem Pegelunterschied von 10dB zwischen zwei Dekaden oder
20dB zwischen der unteren und oberen Dekade problemlos Stimmen und
Instrumente unterscheiden! Den sogenannten Überdeckungseffekt gibt es
nur bei benachbarten Frequenzen unterschiedlichen Pegels.
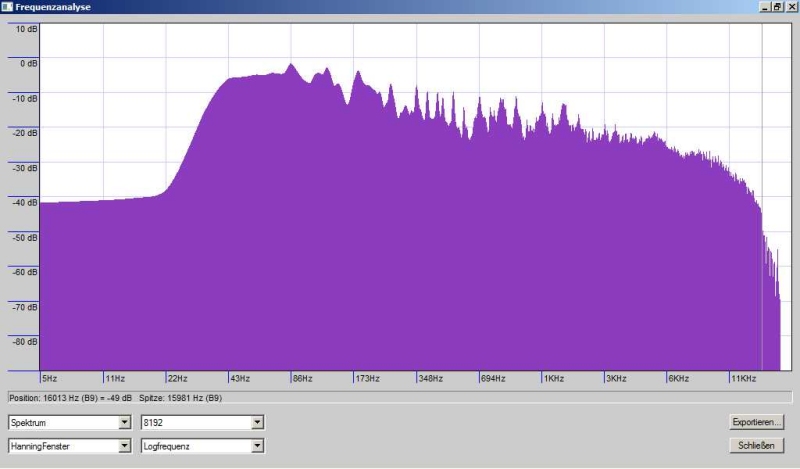
Tina Turner
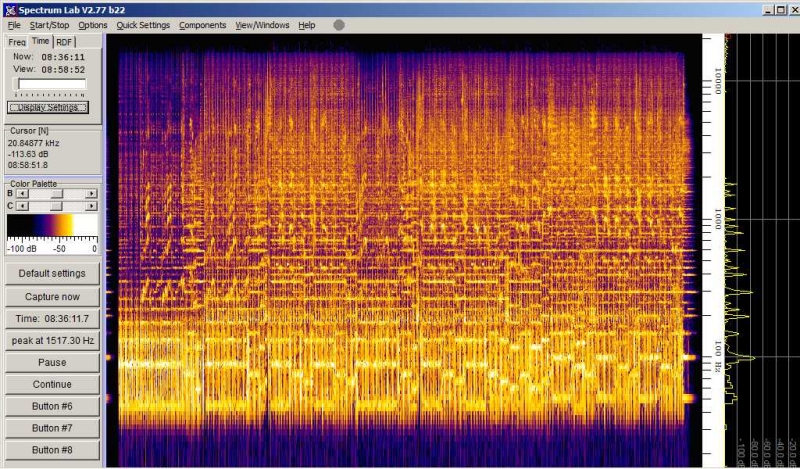
Tina Turner
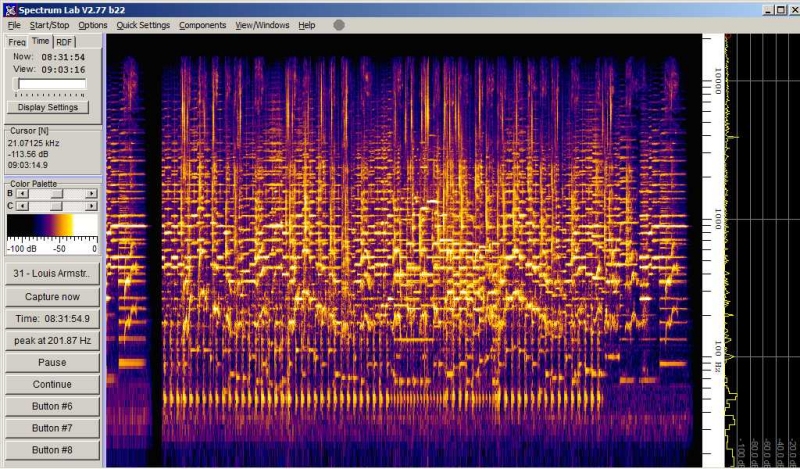
Louis Armstrong
Fazit:
Analysiert man mit einem Mikrofon, kann man Fehler im
Übertragungszweig, bei den Lautsprechern oder der Raumakustik finden.
Ich würde mir gerade noch zutrauen mit einem Spektrogramm Sprache von
Musik zu unterscheiden oder mit rosa Rauschen eine gute von einer
schlechten Akustik zu unterscheiden. Nachhall und Echo sind dabei nicht
zu sehen und müssen mit eigenen Ohren beurteilt werden. Trauen Sie
Ihren Ohren, Musik die gut klingt, sieht auch bei der Analyse gut aus.
Und lassen Sie die Finger von sogenannten Klangreglern, eine Wurst, die
ohne Senf nicht schmeckt, schmeckt mit Senf auch nicht.
P.S.
Die Fourier-Transformation hält noch eine Fussangel bereit. Durch die
Abtastung mit einer festen Sample-Zahl (nicht frequenz-Syncron)
entstehen Spektrallinien, deren Frequenzen tatsächlich NICHT vorhanden
sind! Ein Hanning/Hamming-Fenster glättet die Anzeige, obwohl dieses
Ergebnis dann (weil mathematisch unkorrekt) mit einer reversen
Transformation nicht zurück verwandelt werden kann.
Nachtrag von Wolfgang Hartmann
Die
Erfahrung zeigt, dass Frequenzanalysen bei konzertanter Musik relativ
gleich sind. Mit anderen Worten: Die Messung erfolgt so, dass typische
Stellen für das Gesamtstück analysiert werden. Die Positionierung kann
pro Messung unterschiedlich sein, indem der Cursor an entsprechende
Stellen positioniert und ab dort für 23 sec Laufzeit eine Analyse
erstellt wird.
Sind die Spektren ähnlich kann davon
ausgegangen werden, dass die Anlage des Audiostückes ähnlich ist und in
einem bestimmten großen und kleinen Bereich die Frequenzbereiche
innerhalb des ganzen Stücks gleich sind. Man stellt ein typisches Stück
für den Frequenzbereich des ganzen Stücks.
Es geht dann darum, typische Frequenzspektren gegeneinander mit Quellenangabe zu vergleichen.
Die Analyse einzelner Stimmen oder von Solos ergeben nicht Angaben über den erreichten Frequenzbereich einer Gesamtaufnahme.
Jetzt
mache ich mir Gedanken über die zu benutzende Software und die
Samplerate der Soundkarte soweit es sich nicht um intern eingebaute
Sound-ICs in einer Schaltung handelt, die durch Software nicht
beeinflussbar ist. Die Samplerate von gebräuchlichen Soundkarten sind
48 kHz, 96 kHz und schon recht selten 192 kHz. Dies als Erfahrung mit
div. Dekodierungsprogramm mit einstellbarer Samplerate. Hier wären bei
der Empfänger- und Sofwaretechnik noch höhere Samplerates nützlich; sie
sind aber realistisch nicht zu normalen Konditionen erhältlich.
Wenn
ich nun mit einer Samplerate von etwa 96 kHz Stücke eine Frequenz
um 44 kHz untersuche, habe ich immer vergleichsweise schlechte
Aussichten, weil die Samplerate so nahe (unter dem 10-fachen) der
Samplerate eigentlich ist, dass eine detailgenaue Analyse einer
Schwingung immer Interpolationen liefert und keine auf den Hz-Punkt
genauen Ergebnisse.
Einzelne Solostimmen mit Analysen zu
verfolgen, ist eine sehr reizvolle Tätigkeit; sie zeigen welches
Gesangspotential etwa Louis Armstrong tatsächlich hatte. Der Reiz liegt
in der Analyse von Audiosignalen unterschiedlicher Herkunft.
Wie funktioniert die Spektrumanalyse mit Fouriertransformation (FT), von Heinz D.
Der
Herr Fourier hat herausgefunden, wie man ein kontinuierliches
(=analoges) Signal aus dem Zeitbereich (t) (wie auf dem Oszilloskop) in
ein Frequenzspektum (f) umrechnen kann. Die inverse
Fouriertransformation gestattet das Frequenzspektrum wieder verlustfrei
in den Zeitbereich um zu rechnen (inverse FT). (Nicht mit
AD-DA-Wandlung verwechseln!)
Mit immer billigern Rechnern und
AD-Wandlern lag es nahe die FT für die binäre Verarbeitung anzupassen.
Die Algorytmen der schnellen Fouriertransformation (FFT und iFFT)
werden heute von ALLEN Programmierern und Programmen genutzt. Um es
deutlich zu sagen, die FFT ist genau so gut, wie die FT! Der einzige
Unterschied liegt in der Blocklänge: die FT kann beliebig lange Blöcke
umrechnen, das kann sehr lange dauern, während die FFT-Blocklänge 2^n
sein muss, binär eben.
Um ein (analoges) Signal zu analysieren
müssen wir einzelne Proben nehmen. Das Shannonsche Abtasttheorem zwingt
uns mindestens zwei Proben der höchsten Frequenz zu nehmen. Für ein
NF-Signal (20Hz-20kHz) genügen 44100/48000 Abtastungen pro Sekunde. Bei
16-Bit Auflösung (Standard CD/.wav-File) erhalten wir Werte von +-2^15
= +-32767. In Dezibel umgerechnet: 20*log(Um/U0) = 20*log(32767/1) =
90,3dB. Das ist die maximale Dynamik des 16-Bit-File.
Beispiel:
Wenn das lauteste Signal auf 100dB (phon) eingestellt wird (ganz schön
laut), dann hätte das leiseste Signal (=Rauschen) 10dB. Nun hat ein
leises Schlafzimmer schon ~20-30db. Das 16-Bit-File hat mehr Dynamik,
als man braucht. Ausserdem kommen die meisten Übertragungsketten aus
Plattenspieler, Vorverstärker und Endverstärker nur mit Mühe auf 90dB
Rauschabstand (nicht mit Geräuschabstand verwechseln, da werden hohe
Frequenzen weg gefiltert und die Zahl ist ~20dB besser).
24Bit-Auflösung entsprechen 138dB und so weiter. Die besten
Vorverstärker für Messgeräte quälen den Rauschabstand mit Hilfe von
Chopper-Verstärkern auf ~130dB. Ich glaube nicht, das bezahlbare
Verstärker und AD-Wandler im PC das erreichen.
Nun liegen die
digitalisierten Werte im Speicher und jedes Analyseprogramm holt sich
einen Block (der Länge 2^n) um es durch die FFT zu schieben. Danach
steht exakt die gleiche Datenmenge im Speicher. (An dieser Stelle
können digital einzelne Frequenzen manipuliert werden, um den Block mit
der iFFT wieder in den Zeitbereich zu transformieren - Digitalfilter!)
Die meisten Programme erlauben Blocklängen von 1024 bis 32768 (oder mehr):
Beispiel,
44,1ks/s und 32768 Bit-Blocklänge: 32768/44100 = 0,743s ist die Länge
des untersuchten Signals. Im Speicher steht also für jede Frequenz im
Abstand von 1/0,743s = 1,3458Hz ein Betrag, der die Energie darstellt.
Im 15. Speicher steht die Energie für 20,187Hz, im 150. für 201,87Hz,
im 15000. für 20187Hz usw. Mit der Blocklänge wird die
Frequenzauflösung eingestellt. Das Programm kann demnach alle 0,743s
ein neues Spektrum darstellen. Spannung und Frequenz können linear oder
logarytmisch dargestellt werden (log/log, dB/Oktaven macht Sinn, weil
wir dann auch sehen was wir hören).
Wenn Audacity 24s darstellt,
dann hat es 44100/s * 24s * 16Bit * stereo = 4MB RAM reserviert! Eine
höhere SR (96kHz/192kHz) erhöht die Datenmenge x2/x4. Für die GLEICHE
Frequenzauflösung muss die Blocklänge ebenfalls x2/x4 mal so gross
sein. Ich erhalte das GLEICHE Spektrum mit x4/x16-fachem
Rechenaufwandt!
Da die FFT nicht wissen kann, was im vorigen
oder im nachfolgenden Block steht, entstehen Frequenzlinien mit der
Phase 0°, die z.B. im vorigen Block 180° hatten. Da nur die
|Beträge|ohne Phase dagestellt werden, entstehen Pseudo-Frequenzlinien.
Benötigt man die Daten nur fürs Spktrum, sollte man dem Programm sagen,
das ein Hanning-/Hamming-Fenster mit den Daten verrechnet wird. Damit
werden die Pseudo-Frequenzlinien mehr oder weniger unterdrückt.
Fazit:
Bei
der Spektrumanalyse mit Hilfe der Fouriertransformation handelt es sich
um ein exakte Wissenschaft (reproduzierbare Mathematik). Mehr als
48ks/s und 16-Bit-Wandlung sind für NF-Messungen nicht nötig. Die
Analyseprogramme sind so vielfältig einstellbar, das man damit RICHTIG
MESSEN kann oder eine schöne Darstellung hinbekommt. Und noch ein Wort
zum Frequenzbereich: Die letzte Oktave von 10kHz-20kHz enthält die
5.-10. Oberwelle. Der Energieinhalt ist schon sehr klein. Frequenzen
über 16kHz (musikalisch weniger als die halbe obere Oktave) können
meines Erachtens vernachlässigt werden ohne den Hörgenuss zu schmälern.
Mit vernachlässigen meine ich einen sanften Abfall ab 16kHz, keinen
abrupten Abfall, keine Phasensprünge durch steile Filter/Klangregler,
Verzerrungen schlechter Lautsprecher usw.
Pure-Musik:
Von
einer guten Anlage erwarte ich nicht nur einen geraden Frequenzgang von
20Hz-20kHz (-1dB), sondern auch eine Phasenlage von 0°. Die
Lautsprecher und der Abhörraum dürfen um bis zu +-3dB abweichen, das
lässt sich kaum vermeiden. Meine Lautsprecher, ein Paar 15"-Dipole und
die Beyma-Sateliten finden Sie im Artikel
Lautsprecher-Selbstbau.
Als CD-Player benutze ich einen Bluray-Player, der m.E. den besten
DA-Wandler hat. Dahinter kommt direkt nur ein PA-Endstufenblock ohne
Filter, wie Musiker sie benutzen. Das alles hat <1000€ gekostet, ich
habe noch nichts Besseres gehört.
Mit einer Mess-CD, einem
Spektrumanalyser und einem guten Messmikrofon kann dann alles optimal
aufeinander eingestellt, aufgestellt und abgestimmt werden.