Versuche mit der RLC-Box
Bei Modul-Bus gibt es nun die RLC-Box in zwei Versionen, Standard und
Deluxe. Roger hat mit eine Vorversion der RLC-Box Deluxe geschickt,
noch mit einer roten Platine, in der Serie ist sie blau. Das Gerät
enthält drei 24-stufige Drehschalter für Kondensatoren von 10 pF bis
1000 µF, Spulen von10 nH bis 150 mH und Widerständen von 10 R bis 820 k
(Standard) bzw. 0 R bis 10 M (Deluxe). Die Deluxe-Version hat zwei
Zehngang-Potis mit 1 k und 100 k für den unteren Bereich und
Widerstände von 120 k bis 10 M für den oberen. R und C sind jeweils
doppelt bestückt und haben einen unteren und einen oberen Bereich,
sodass insgesamt 48 Kondensatoren und 48 Spulen vorhanden sind.
Roger hat umfangreiche Informationen und Videos zu Messungen mit der
RLC.Box zusammengestellt und zeigt Messungen zu RLC-Filtern und
Resonanzkreisen mit unterschiedlicher Dämpfung. Man kann sich
vorstellen, dass es im Elektronik-Labor immer wieder mal Situationen
gibt, in denen die beste Dimensionierung für eine Schaltung gesucht
wird. Oft scheitert etwas an den nicht vorhandenen Bauteilen. Aber mit
der RLC-Box hat man alles bequem zur Hand, kann das entsprechende
Bauteil finden, und weiß dann, was bestellt werden muss.
Eine Frage ging mir schon länger durch den Kopf: Kann man mit einer
üblichen Festinduktivität ein brauchbares CW-Filter im Bereich 700 Hz
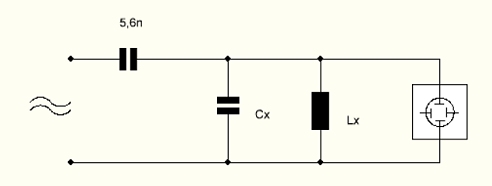
bauen? Mit der RLC-Box ist die Sache schnell zu klären. Es gibt einen
Schalter, mit dem man L und C parallel schalten kann. Zusätzlich habe
ich einen externen Koppelkondensator mit 5,6 nF zum Sinusgenerator
verwendet. Direkt am Schwingkreis lag das Oszilloskop mi dem
10:1-Tastkopf mit dem Innenwiderstand 10M.
Gar nicht lange überlegen, sondern einfach probieren, das bringt die
schnellste Lösung mit der RLC-Box. So habe ich als mögliche Werte 150
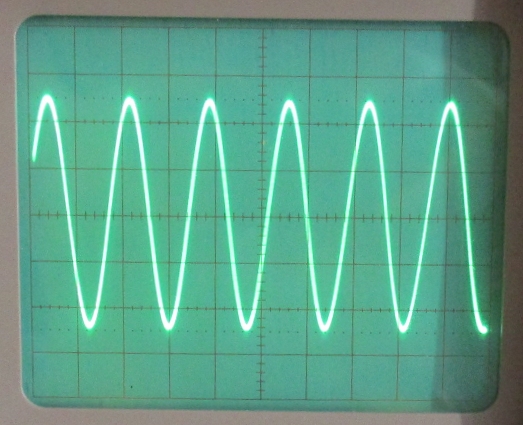
mH und 330 nF gefunden. Die Resonanzfrequenz liegt dann bei 700 Hz. Und
weil mein Oszilloskop Hilfslinien bei -3dB hat, ist auch die Bandbreite
schnell bestimmt. Die -3dB-Punkte liegen bei 600 Hz und bei 800 Hz, die
Bandbreite ist also 200 Hz. Daraus ergibt sich eine Kreisgüte von Q =
3,5.
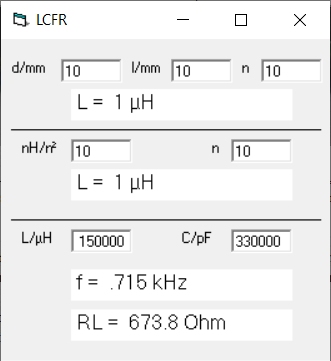
Mit meinem VB-Programm LCFR
komme ich auf eine Resonanzfrequenz von 715 Hz und einen induktiven
Widerstand von 674 R. Der Resonanzwiderstand sollte dann um den Faktor
Q höher liegen, also bei ca. 2,4 k. Umgekehrt kann man versuchen, den
Spulenwiderstand abzuschätzen. Er müsste um den Faktor Q kleiner sein
als der induktive Widerstand, also etwa bei 190 R liegen. Die
verwendete Spule (Fastron 11P mit 150 mH) gibt es auch bei Reichelt.
Dort findet man die technischen Daten. Der Spulenwiderstand ist mit 205
R angegeben.
Könnte es noch eine bessere Dimensionierung geben? Allgemein geht man
davon aus, dass eine hohes L/C-Verhältnis meist zu eine hohen Güte
führt. Aber ganz sicher ist das nicht. Fastron könnte z.B. für weniger
Induktivität dickeren Spulendraht verwenden, und dann könnte es doch
wieder anders aussehen. Mit der RLC-Box ist das schnell getestet: Mit
100 mH und 470 nF messe ich eine Resonanz bei 680 Hz. Die Bandbreite
bleibt bei ca. 200 Hz. Diese Kombination ist also im Rahmen der
Messgenauigkeit gleich gut. Die verwendete Spule hat laut Datenblatt
einen Drahtwiderstand von 155 R. Noch viel bessere Werte könnte man nur
bei einer wesentlich größeren Spule auf einem Trafokern erwarten.
Fazit: Eine Bandbreite von 200 Hz ist für ein CW-Filter sinnvoll. Mit
zwei oder drei Kreisen könnte man also durchaus ein brauchbares
LC-CW-Filter bauen. Bisher habe ich für den Zweck ein aktives Filter verwendet.
