 Interessante OPAmp Schaltungsvarianten
Interessante OPAmp Schaltungsvarianten Interessante OPAmp Schaltungsvarianten
Interessante OPAmp SchaltungsvariantenAuf der Elo Webseite http://www.elo-web.de/elo/grundlagen-ausbildung/operationsverstaerker findet man eine umfangreiche
Basis zu Operationsverstärkern. Darauf aufbauend und in der Annahme, dass sie
schon etwas Praxis mit Experimenten gewonnen haben, möchte ich folgende
Schaltung vorstellen:
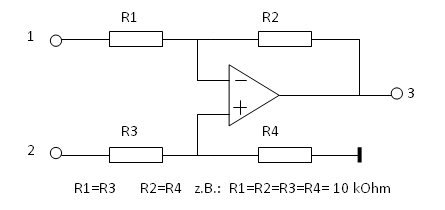
Es ist ein
Differenzverstärker. Wenn vor den Eingängen 1 und 2 noch je ein Spannungsfolger
vorgeschaltet wäre, handelte es sich um den einfachsten Fall des
Instrumentenverstärkers. Der Eingangswiderstand wäre dann sehr hoch und
symmetrisch, aber für die folgenden Betrachtungen braucht man dies nicht. Ein
Beispiel siehe: http://www.elo-web.de/elo/bauprojekte/schaltungstechnik/der-rc-generator-einst-und-jetzt
1.
Zur
Erinnerung nochmals die Grundregeln für die einfache Anwendung von OPAmp’s:
1.1 Vernachlässigbarer
Eingangsstrom, was bei
FET-Eingang, am Beispiel vom TL072 mit 5 pA Bias gut erfüllt ist. Zur
Relativität von Größen: 5 pA sind noch
5e-12/1,6e-19
= 30 mio Elektronen pro Sekunde die in den Eingang fließen.
Aber
selbst an einem 1 MOhm Widerstand fällt dann nur eine Spannung von
5 uV ab.
Am Ausgang ergäbe sich aber schon eine Spannungsänderung von 1V.
Wir kommen
damit unmittelbar zur Regel 2.
1.2 Große Leerlaufverstärkung. Für praktische Anwendungen genügt schon
eine Verstärkung von 20000….200000, die der TL072 als typischen Wert auch hat. Daraus
ergibt sich die Regel, dass bei einer Ausgangsspannung innerhalb der Speisespannungsgrenzen, also im linearen
Aussteuerbereich:
Die Spannung am + Eingang ist
gleich der Spannung am – Eingang.
Ein Beispiel: Die Ausgangsspannung sei 4V, also ist
die Eingangsspannungsdifferenz 4 /
200000 = 20 uV, was tatsächlich praktisch gegen NULL geht.
1.3 Der Ausgangswiderstand soll klein sein gegenüber dem
Lastwiderstand.
Das
ist beim TL072 bis 2 kOhm Lastwiderstand
gut erfüllt.
2. Die Schaltung wird nun abgewandelt zu:
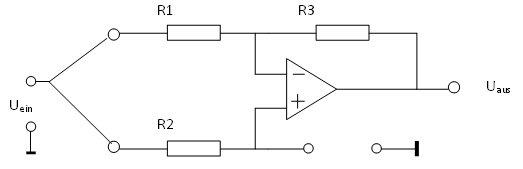
![]() Anstelle von R4 werden folgende Bauelemente
eingefügt und die sich ergebende Auswirkung diskutiert.
Anstelle von R4 werden folgende Bauelemente
eingefügt und die sich ergebende Auswirkung diskutiert.
Fall 1: R4 ist noch vorhanden
Fall 2: kein Bauelement, R4 fehlt also
Fall 3: ein Schalter offen, bzw. geschlossen
Fall 4: eine Diode
Fall 5: Ein Kondensator C oder eine Induktivität L
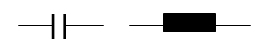
Nachfolgend wird immer Regel 1.2
angewandt.
2.1 R4 ist noch
vorhanden
Formeln
für die Berechnung finden sie z.B. unter
http://www.elektronik-kompendium.de/sites/slt/0210153.htm
Wir nehmen einen Fall
praktisch durch, da Formeln alleine nicht so gut zum Verständnis beitragen.
Natürlich ist die Mathematik später für die Dimensionierung unerlässlich.
R1…R4 ist 10 kOhm, Uin
sei 2 V. Durch den Spannungsteiler R2/R4 liegt am + Eingang des OPAmp dann 1V.
Mit Regel 2 liegt auch am – Eingang 1V. Also liegt an R1 auch 1V. An R3 demzufolge
auch, da der gleiche Strom ja durch R1 und R3 fließt. Als Konsequenz muss also
auch die Spannung Uaus Null Volt sein.
Mit Uin ist 4 oder 6V, jedes Mal ist die
Ausgangsspannung Null!
Die Verstärkung ist also
NULL.
Das ist auch gut so, da, wenn
keine Spannungsdifferenz zwischen den beiden Eingängen vorliegt (sie sind ja
verbunden), so soll es auch keine Reaktion des Ausgangs geben.
Man spricht von der
Gleichtaktunterdrückung oder „Common mode rejection ratio“ CMRR das in den
Datenblättern angegeben ist, die ja fast nur in Englisch vorliegen.
2.2 R4 fehlt, die Symmetrie von 2.1 ist heftig gestört.
Uin sei wieder 2V. Da kein Eingangsstrom am + Eingang fließt, er
ist ja hochohmig, , so liegen 2 V am + und also auch am – Eingang. Es fließt
also kein Strom durch R1 und als Konsequenz auch nicht durch R3. Die
Ausgangsspannung ist also auch 2 V.
Die Verstärkung ist also +1
2.3.1 Der
Schalter ist offen. Es gilt das unter 2.2 Beschriebene
2.3.2 Der
Schalter ist geschlossen.
Uin sei wieder 2V.
Am + Eingang liegt also 0 Volt und damit auch am – Eingang. An R1 liegt also 2
V. Deshalb auch an R3.
Die Ausgangsspannung ist also
-2V.
Die Verstärkung ist -1. Es
ist die klassische Inverterschaltung.
Jetzt wird es ein wenig
sichtbarer was gemeint ist mit „Interessanten Schaltungsvarianten“
Durch öffnen oder schließen
des Schalters kann die Verstärkung von +1 auf -1 umgeschaltet werden. Eine
einfachere Phasenumkehrschaltung ist kaum denkbar, die für viele Zwecke
eingesetzt werden kann, z.B. um einen Kanal eines Stereoverstärkers in der
Polarität umzuschalten. Sehr praktisch für die Ermittlung der richtigen Polung
der Lautsprecher.
Bei richtiger Polung hört man
die Bässe zwischen den Lautsprechern.
2.4 Eine Diode ist an Stelle von R4 verbaut
Jetzt geht es schon schneller
voran mit der Erklärung.
Für positive Spannungen ist
die Verstärkung +1 . Die Diode ist gesperrt
Für negative Spannungen ist
die Verstärkung -1 . Die Diode ist jetzt leitend
Sie wissen doch noch: minus x
minus gibt +.
Diese Schaltung ist also ein
Vollweggleichrichter mit nur einer Diode.
2.5 Ein Kondensator oder eine Spule ist eingefügt.
Für tiefe Frequenzen ist die
Impedanz des Kondensators sehr hoch, wie etwa der offene Schalter. Für hohe
Frequenzen sehr niedrig, entsprechend dem geschlossenen Schalter.
Die Verstärkung wechselt also
über die Frequenz von +1 auf -1.
Bei einer Spule ist es
umgekehrt, die Verstärkung wechselt von -1 auf +1.
Genau genommen ändert sich
nur die Phase um 180°. Die Amplitude der Ausgangsspannung bleibt konstant. Die
Erklärung folgt weiter unten.
So eine Schaltung nennt man
einen Allpass. Mit 8 Allpässen lässt sich der gesamte Hörbereich um 90° in der
Phase verschieben. Radioamateure brauchen eine solche Schaltung um SSB Signale
zu erzeugen.
Es ist auch ein RC Generator
möglich, der Sinus und Cosinus Signale gleichzeitig erzeugt. Ein Beispiel im
nächsten Beitrag.
3.
Graphische Methode zu beweisen, dass der
Allpass nur die Phase dreht,
aber die
Amplitude konstant bleibt.
Relativ leicht einzusehen sind die Grenzfälle bei 0
Hertz und so hoher Frequenz, dass die Impedanz des Kondensators nur mehr, sagen
wir, 1/1000_ stel der Widerstandes ist. Dass die Verstärkung von +1 auf -1 geht
ist schon von dem vorher gesagten klar, es muss nur noch die Amplitudenkonstanz bewiesen werden.
Es ist dazu erforderlich, die bisher gebrauchte
Gleichstromtechnik und rudimentäre Wechselstromtechnik zu erweitern und das
Verhalten von Kondensatoren und Induktivitäten bei Wechselstrom, was unter
Punkt 4 dargestellt wird, nämlich das Spannung und Strom durch das Bauelement
um 90° phasenverschoben sind, zu beweisen. Man nennt solche Bauteile auch
Blindwiderstande, die nicht mehr mit R sondern mit X bezeichnet werden. Oft
findet man Rc oder Rl, was aber nicht ganz exakt ist, aber dazu
später.
Ich wähle mit
Absicht graphische Methoden, da sie augenscheinlich, ohne Mathematik, erfasst
werden können.
Die Schaltung unter Punkt 2 kann äquivalent wie folgt
gezeichnet werden. Einmal wird die Eingangsspannung verstärkt um +1 und das
andere Mal um -1. Daran angeschlossen ist das RC Glied R2 und der Kondensator
C. Der Strom i fließt durch beide Elemente. Die Ausgangspannung wird an der
Verbindungsstelle zwischen R2 und C abgenommen.
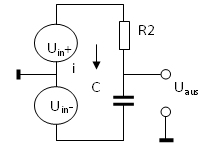
Die Spannungen werden als Pfeile dargestellt und die
Spitze soll die + Richtung, das andere Ende die – Richtung angeben.
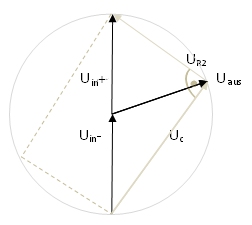
Die Spannung Uaus
ist an jedem Punkt des Kreisumfanges natürlich gleich groß, nur der Winkel
zwischen Uein und Uaus ist verschieden groß. Bei tiefen
Frequenzen fast 0°, bei hohen Frequenzen fast 180°. Das ist damit bewiesen.
4. Beweis
dass der Wechselstrom durch den Kondensator der Spannung um 90° voreilt
Im Wiki findet sich eine
Menge darüber, nur der Beweis nicht.
http://de.wikipedia.org/wiki/Kondensator_%28Elektrotechnik%29
http://de.wikipedia.org/wiki/Blindwiderstand
http://www.uni-protokolle.de/foren/viewt/156006,0.html
Beim letzten Link hat schon
einmal jemand in 2007 danach gefragt.
Normalerweise kann das mit
Differential und Integralrechnung bewiesen werden. Ich möchte es aber
allgemeinverständlich, aber natürlich einwandfrei richtig beweisen.
Ich möchte ausdrücklich
betonen, dass ich annehme, dass viele
Leute, die math. gut vorgebildet sind, sich bei der Lektüre dieses Abschnittes
langweilen werden. Aber meine Intention ist es eben, es allgemein verständlich
darzustellen. Aber man kann den Abschnitt ja überlesen.
Ein Kondensator ist ein
Stromspeicher. Schickt man Strom eine zeitlang hinein, so erhöht sich die
Spannung am Kondensator. Wie schnell sich die Spannung erhöht hängt von der
Kapazität des Kondensators ab und wie hoch der Strom ist.
Es existiert also eine
Beziehung zwischen diesen 4 Werten, die, kann man sagen, gut bekannt, bzw. in
Erinnerung ist.
Uc *
C =
i * t
Uc…. Spannung am Kondensator
C…….die
Kapazität desselben
i……..der
Strom, der fließt
t……..die
Zeit, wie lange der Strom fließt
Ein passendes Beispiel ist
das Blitzgerät in einem Photoapparat älterer Bauweise, wo nachdem es blitzte,
ein Pfeifen oder Summen hörbar war, bis die Ladekontrolllampe aufleuchtete und
damit der Aufladevorgang beendet war.
Typisch war eine Zeitdauer
von etwa 10 Sekunden. Die Spannung
am Kondensator mit 300 uF
war dann etwa 300 V. Ich habe so was aus Einmalkameras, wo nur eine 1,5
V Batterie verwendet wird.
Der Strom i war also im
Mittel 300 uF * 300 V / 10 Sekunden = 9
mA
Das ist ein sehr kleiner
Strom an sich, aber berühren sie nie so
einen auf 300 V aufgeladenen Blitzkondensator. Es könnte tödlich sein!
Wir wandeln die Formel etwas
ab für eine bestimmte Zeitdauer und nennen diese dt.
Folgedessen wird auch die
Spannung am Kondensator auch nur um eine gewisse Spannung steigen und nennen
diese dU. Die Formel sieht also so aus:
dU = i * dt / C
Man kann auch sagen: Links
des „=“ steht die Wirkung , auf der rechten Seite der Gleichung die Ursache.
Die Wirkung, das Ergebnis
einer Aktion, kommt immer *nach* der Ursache (man diskutiert das
übrigens in der Quantenphysik, ob man sich nicht etwas Wirkung vor der Ursache
ausborgen kann in Analogie zu einem Bankkredit).
Diese Beziehung verwenden wir
nun in einem Excelsheet. dt wählen wir ziemlich klein und stellen die Spannung
U am Kondensator dar, die aus der *Summe*
der einzelnen Ladespannungsschritte dU gebildet wird. Wenn alles gut geht
sollte sich dann die 90° Beziehung zwischen Spannung und Strom zeigen!
Einen sinusförmigen Strom mit
50 Hz nehmen wir als Stimulus / Ursache. Alle
0,5 ms wird berechnet um welchen Betrag sich die
Spannung am Kondensator geändert hat. In der Integral- als auch
Differentialrechnung ist diese Zeitspanne unendlich klein, aber nicht NULL!
Eine 50 Hz Periode dauert 20
ms. Wir schauen also 40 Mal je Periode nach was geschieht.
Dies reicht aus, sonst würde
z.B. DSP nicht funktionieren. DSP Prozessoren kennen auch keine höhere
Mathematik. Dort macht es die Software, aber in endlich kleinen und nicht
unendlich kleinen Schritten.
Nebenbemerkung: Sir Isaac
Newton und Leibnitz, die etwa zur gleichen Zeit die Differential- und
Integralrechnung erfunden haben, hätten diese IMHO sicher erst später entdeckt,
hätten sie damals schon Computer zur Verfügung gehabt, wie wir es heute haben.
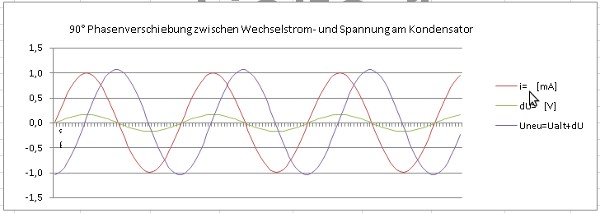
Die Exceldatei ist im Bericht
includiert. Die Eingabefelder sind markiert und sie können alle Werte verändern.
Man sieht deutlich, dass du
noch in Phase mit dem Strom i ist. Erst die *Summierung* (die Integration) der einzelnen du macht
dann die 90° Phasenverschiebung aus. Die Spannung (Wirkung) eilt dem Strom
(Ursache) nach. Man könnte sogar sagen, dass ist doch alles ganz logisch! Genau
das wollte ich erreichen und zeigen, dass hinter höherer Mathematik kein
Geheimnis verborgen ist.
Analog dazu reagiert eine
Induktivität bei Wechselstrom. Nur ist dort die Spannung die Ursache und der
Strom die Wirkung. Der Strom eilt der Spannung nach. Deshalb sehe ich keine
Notwendigkeit das weiter ausführen.
L1-----R--+--R----C------L2
!
!
Glimmlampe
!
!
L2-----R--+--R----C------L3