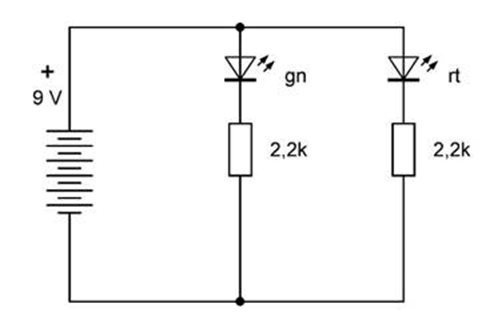
2.2 Rot und Grün
In dieser Schaltung werden zwei LEDs mit
je einem Vorwiderstand parallel an eine Spannungsquelle angeschlossen.
Das bedeutet, dass an jeder
LED-/Vorwiderstandsreihe die volle Eingangsspannung in der Höhe von 9 Volt
anliegt. Die Spannung fällt dann jeweils an den LEDs und Vorwiderständen ab und
teilt sich so auf. Insgesamt müssen sich nach dem 2. Kirchhoff‘schen Gesetz
(die Summe aller Spannungen in einer Masche ergibt 0 Volt) die Eingangsspannung
und die jeweiligen Spannungsabfälle pro Reihe aufheben.
Dass sich der Spannungsabfall an einer
LED nur schwer berechnen lässt, haben wir im Elektronik-Labor hier gesehen. Deshalb
halten wir uns nicht lange mit Überlegungen auf und simulieren die Schaltung
wieder in EveryCircuit. Dies aber mit
so präzisen Werten wie möglich.
LED-Vorwärtsspannungen mit dem Bauteiletester ermitteln
Mit dem Bauteiletester LCR-T4 können wir die Vorwärtsspannung einer LED einfach ermitteln. Anstatt die üblichen Durchschnittswerte für grüne LEDs (2,0 Volt) und rote LEDs (1,8 Volt) in die Simulation einzusetzen, nehmen wir die vom Bauteiletester ermittelten Werte. Das sind 1,97 Volt für die grüne und 1,90 Volt für die rote LED. Es handelt sich nur um kleine kleine Abweichungen aber sie sind immerhin vorhanden und sollen daher berücksichtigt werden.

Würden wir es ganz genau machen wollen, müssten
wir auch die tatsächlichen Werte der Widerstände mit dem Bauteiletester oder
Multimeter ermitteln, die bei diesem Typ um +/- 5 Prozent vom Nennwert
abweichen können. Aber darauf verzichten wir, um es uns nicht zu kompliziert zu
machen. (Anmerkung
BK: Eigentlich müsste man wissen, bei welchem Strom der Tester die
Diodenspannung bestimmt, denn sie Spannung ist ja geringfügig vom Strom
abhängig.)
Simulation in EveryCircuit
Die Simulation zeigt folgendes Bild:
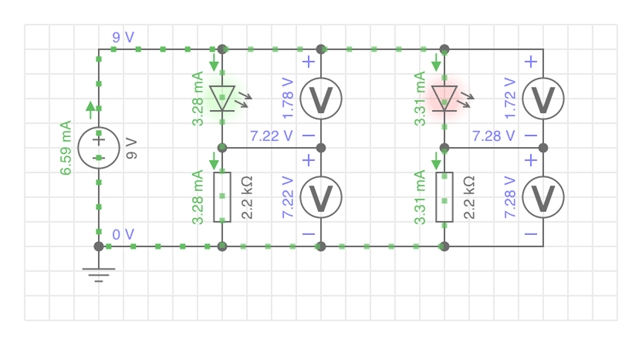
Die Spannungsabfälle ergeben sich aus den
jeweiligen LED-Widerständen und Vorwiderstandswerten. Da in einer
Reihenschaltung der Spannungsabfall jeweils dem höchsten Widerstand folgt,
ziehen die beiden 2,2 kOhm Widerstände etwas vom Spannungsabfall an den LEDs an
sich. So ergeben sich die jeweilgen Spannungsaufteilungen in den beiden Reihenschaltungen.
Und nun ab aufs Steckbrett
Nun wollen wir prüfen, welche
Spannungsabfälle in der realen Schaltung am Steckbrett auftreten und stecken
die Bauteile:

Mit dem
Multimeter messen wir die Spannungsabfälle an den Bauteilen und stellen sie
denen aus der Simulation gegenüber:
|
Bauteile |
Spannungsabfälle simuliert (V) |
Spannungsabfälle gemessen (V) |
|
LEDgrün |
1,78 |
1,95 |
|
LEDrot |
1,72 |
1,88 |
|
Vorwiderstandgrün |
7,22 |
7,04 |
|
Vorwiderstandrot |
7,28 |
7,10 |
|
|
|
|
Wir können zufrieden sein, Simulation und
Realität liegen eng beinander 🙂
Welche Ströme fließen in unserer Schaltung?
Wir haben jeweils einen Teilstrom pro
LED-/Vorwiderstandsreihe und einen Gesamtstrom, der nach dem 1. Kirchhoff‘schen
Gesetz (die Summe aller Ströme in einem Knoten ergibt 0 Ampere) mit gleicher
Stromstärke in beide Reihenschaltungen ein- und wieder ausfließt.
Den Gesamtstrom und beide Teilströme können
wir mit der Formel für die Ermittlung eines LED-Vorwiderstandes berechnen:
Rv =
(UE - Uf)/ILED
Vorwiderstand =
(Eingangsspannung - Vorwärtsspannung)/LED-Strom
In die Formel eingesetzt und diese
umgestellt, ergeben sich bei einer Eingangsspannung von 9 Volt und den mit dem
Bauteiletester ermittelten Vorwärtsspannungen folgende Teilströme, die wir den
simulierten und gemessenen Werten gegenüberstellen:
|
Reihenschaltung |
Teilströme berechnet (mA) |
Teilströme simuliert (mA) |
Teilströme gemessen (mA) |
|
ILED grün + Vorwiderstand |
3,2 |
3,28 |
3,24 |
|
ILED rot + Vorwiderstand |
3,2 |
3,31 |
3,26 |
Der Gesamtstrom ergibt sich aus ILED
grün + ILED rot:
|
Modus |
Gesamtströme (mA) |
|
Berechnung |
6,40 |
|
Simulation |
6,59 |
|
Messung |
6,49 |
Vergleichen wir diese Werte, können wir
auch hier zufrieden sein. Alles eng beinander. Alles für die Praxis tauglich 🙂

Messung des Gesamtstromes in der Schaltung mit dem Multimeter.

Stabilisierte Spannungsversorgung mit dem Labornetzgerät
Weitere Messungen von Jürgen Heisig
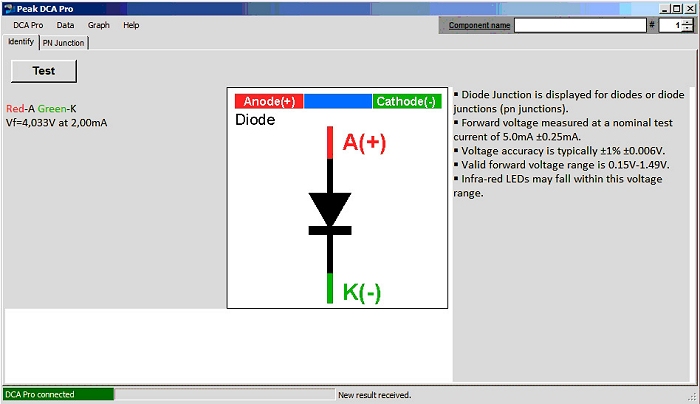
Ich habe den Beitrag von Andreas Thaler zum Anlass genommen, einmal die Ergebnisse von 2 Komponententestern gegenüber zu stellen. Der eine Tester ist ein chinesischen Produkt, sehr ähnlich (wenn nicht gleich) dem von Andreas Thaler. Der zweite Tester ist ein DCA Pro (DCA75) von Peak und um einen vielfaches teurer. Dafür lässt er sich mit dem PC bedienen und kann die Kennlinie aufnehmen. Die Kapazität der Diode zeigt er nicht an...
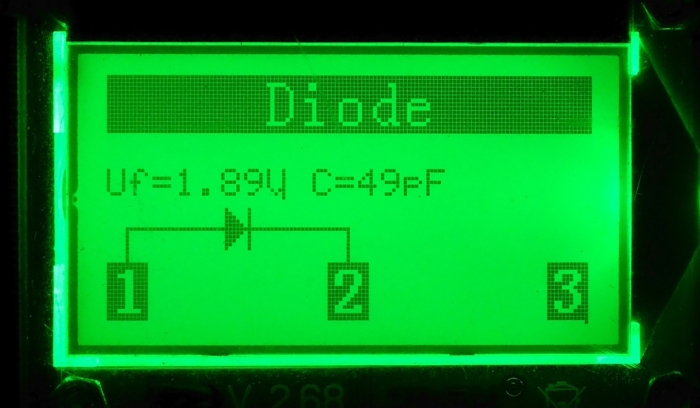
Rot
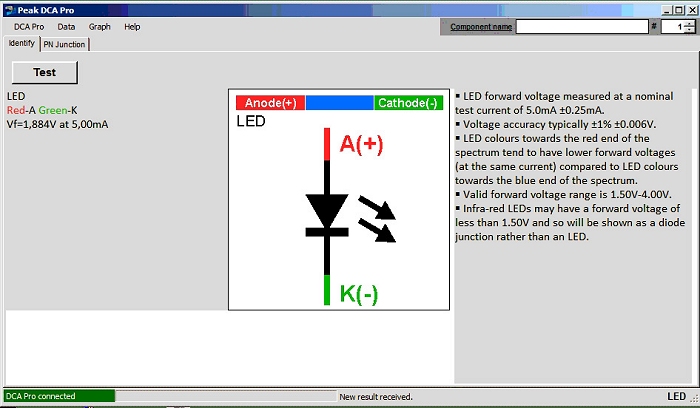
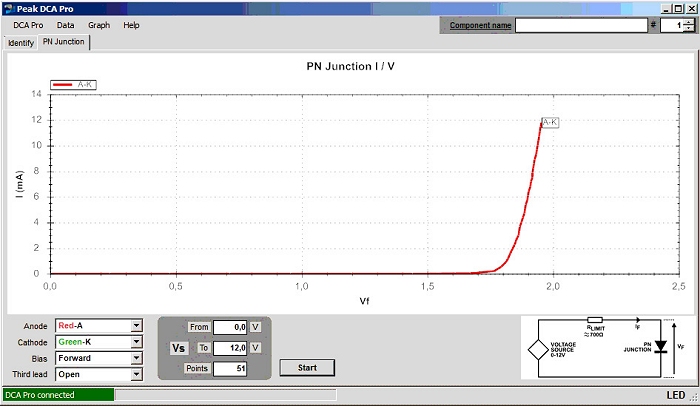
Getestet wurden eine rote LED, eine grüne LED und noch eine grüne LED mit internem Vorwiderstand - alle 5mm. Wie man an den Ergebnissen sieht, stimmen die Ergebnisse bei den Zahlen recht genau überein - nur die LED mit internem Rv tanzt etwas aus der Reihe. Hier machen sich Unterschiede im Messstrom eben besonders bemerkbar.
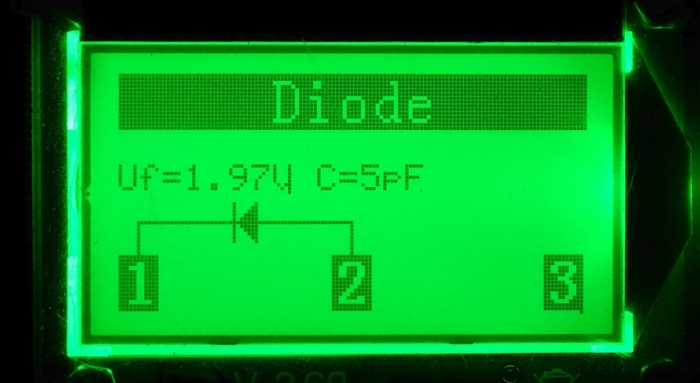
Grün
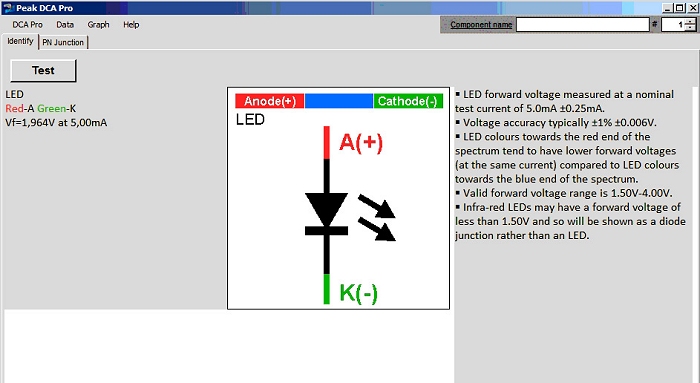
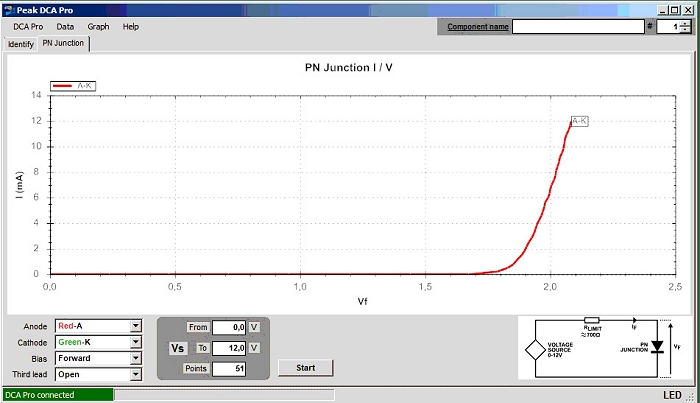
Die mit dem DCA aufgenommenen Kennlinien zeigen deutlich, wie berechtigt Ihre Anmerkung zum Messstrom ist - die Bandbreite von VF ist erheblich. Der DCA Pro misst nur bis 12 mA - real ist aber mindestens 20mA erlaubt und die Bandbreite von Vf damit noch größer.
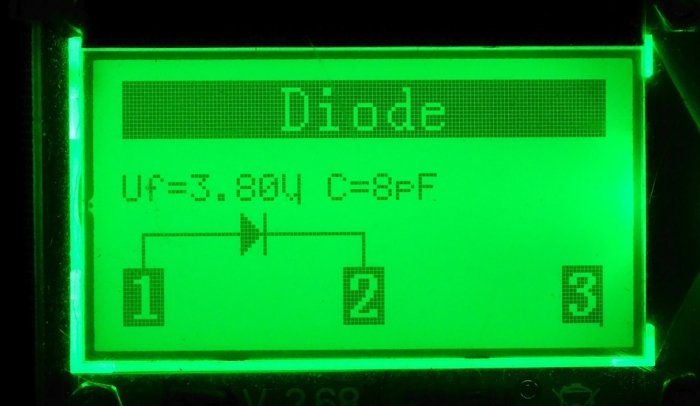
Grün mit Widerstand
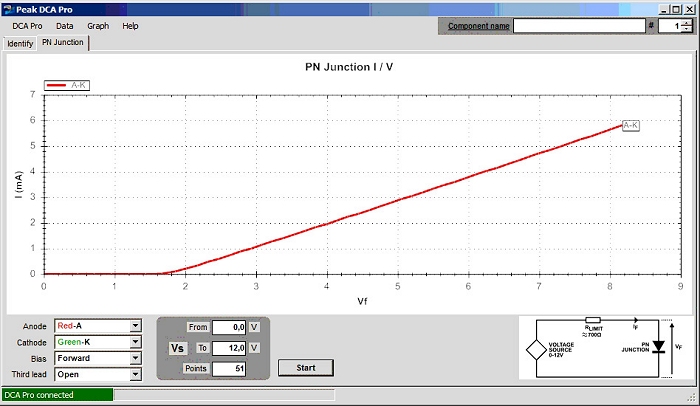
Eine Anmerkung zu den Messwerten allgemein: Wie bei allen Digitalen Messwerten ist der letzten Stelle _immer_ zu misstrauen. Der DCA Pro treibt es mit seinen 3 Nachkommastellen auf die Spitze - das kann man in diesem Zusammenhang nicht ernst nehmen. In der realen Welt hat das alles keine Bedeutung, niemand setzt einen so bestimmten/berechneten Vorwiderstand ein. Man nimmt einfach den nächsten Normwert - und bringt damit deutlich mehr "Ungenauigkeit" ins Spiel, als die Variation von Vf es könnte.
Den eigentlichen Mehrwert im Beitrag von Andreas Thaler sehe ich in dem Vergleich Simulation gegen reale Welt. Die heutigen Simulationsprogramme sind sehr gut - trotzdem eben nur eine Simulation, die man immer wieder mit der realen Welt abgleichen muss. Nach meinen Erfahrungen mit LTSpice funktioniert einiges in der Simu, aber nicht real - und nicht alles, was real funktioniert, lässt sich in der Simu ohne Weiteres nachvollziehen.