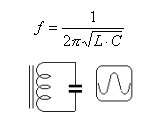Schwingkreis und Resonanzfrequenz

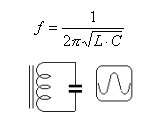
Für einen Schwingkreis mit der Induktivität L und der Kapazität C ergibt sich die Resonanzfrequenz f:

Resonanzfrequenz = 1 / ( 2 * Pi * (Induktivität * Kapazität)^1/2)
f = 1 / (2 * Pi *( L * C)^1/2)
0,159 Hz = 1 / ( 2 * Pi *(1 H * 1 F)^1/2)

Der induktive Widerstand RL beträgt bei dieser Frequenz:

RL=2 * Pi * f * L
RL= 2 * Pi * 0,159 Hz * 1 H
RL = I Ohm

Gesucht:  Resonanzfrequenz f,   Kapazität C,    Induktivität L

Resonanzfrequenz berechnen


Beispiel: Wie groß ist die Resonanzfrequenz für einen Schwingkreis mit L = 300 µH und C = 500 pF?

f = 1 / (2 * Pi *( L * C)^1/2)
f = 1 / (2 * Pi *( 300 µH *500 pF)^1/2)
f = 410.936 kHz  

Und wie groß ist der induktive Widerstand im Resonanzfall?

RL = 2 * Pi *( L * f)
RL = 2 * Pi *( 300 µH * 410.936 kHz )
RL = 774.6 Ohm

Der Online-Rechner erwartet die Kapazität in pF und die Induktivität in µH, weil dies die meisten Fälle abdeckt. Den induktiven Widerstand zu wissen ist nützlich, um die Schwingkreisgüte abzuschätzen. Wenn man den Kreis parallel mit einem zehnfach größeren ohmschen Widerstand belastet, ist die Güte Q = 10.

Eingabe: Widerstand =
µH
Eingabe: Kapazität =
pF

Ergebnis: Grenzfrequenz  =
kHz

Induktiver Widerstand  =
Ohm


Kapazität berechnen

Man hat eine bekannte Induktivität (10 µH) und braucht eine bestimmte Grenzfrequenz (3500 kHz). Wie groß muss die Kapazität gewählt werden?

C = 1 / (L*(2 * Pi * f)^2)
C = 1 / (10 µH * (2 * Pi * 3500 kHz)^2)
C = 207 pF 

Eingabe: Widerstand =
µH
Eingabe: Grenzfrequenz =
kHz

Ergebnis: Kapazität =
pF

Induktivität berechnen

Man hat einen bekannten Kondensator (100 pF)  und findet eine Resonanzfrequenz von 6000 kHz. Wie groß ist die Induktivität?

L= 1 / (C*(2 * Pi * f)^2)
L = 1 / (100 pF * (2 * Pi * 6000 kHz)^2)
L = 7 µH 

Eingabe: Kapazität =
pF
Eingabe: Resonanzfrequenz =
kHz

Ergebnis: Induktivität =
µH

Siehe auch: Die kleine Spulenkunde in der Bastelecke

weiter
zurück