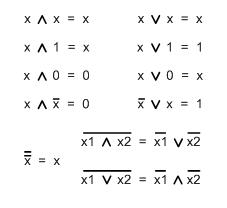|
Digitale Schaltungen - ganz einfach ausprobieren |
|
von Rüdiger Rennert, www.u-r-rennert.de/dig/dig_schalt1.htm
Digitaltechnik ist die Basis nahezu aller neuen Techniken.
Natürlich für jeden verständlicher Weise im Computer. Aber auch in vielen anderen
Geräten des täglichen Gebrauchs wird Digitaltechnik benötigt, sei es das Handy, der
iPod, der elektronisch Bilderrahmen, das Navi usw. Auch auf dem klassischen Bereich der
analogen Technik, z.B. dem Fernsehen, geht es ab 2012 digital zu. Neue Autos sind
vollgestopft mit Elektronik, wie ABS (Anti-Blockier-System), ASS (Anti-Schlupf-System),
ESP (Elektr.-Stabilitäts-Paket), elektr. Zündsystem, Regensensor zur Steuerung
des Scheibenwischers usw.
Auch Kinderspielzeug piept und
spielt Musik - überall stecken kleine digitale Schaltungen dahinter,
daraus folgt, will mann nicht hoffnungslos zurückbleiben,
sich irgendwie mit dieser Technik zu beschäftigen.
Diese Seiten sollen eine Möglichkeit bieten, an kleinen Versuchen einige Beispiele der Digitaltechnik zu ergründen - also so "learning by doing".
Was braucht man?
3 kleine Taster, ein paar Widerstände, wenige Kondensatoren, 2(3) LED's,
einen npn-Transistor und einen
digitalen Schaltkreis 4011.
Weiterhin ist es sinnvoll, ein Steckbrett einschließlich
der Betriebsspannungsversorgung von 9 Volt zum
Aufbau der Versuche zu nutzen, man spart das Löten, ginge prinzipiell aber auch.
So ein Steckbrett könnte man z.B. aus einem Adventskalender von "Conrad" schon haben.
Die Schaltungen brauchen maximal nur den einen Schaltkreis.
-

So etwa sieht der Schaltkreis 4011 aus
kann man bei "Conrad" kaufen; (Best.-Nr.: 172570 - 62; 0,52 EURO)
Den kann man als Taster verwenden:
(kann man auch bei "Conrad" kaufen; (Best.-Nr.: 701749 - 62; 0,15 EURO))
Neben der Realisierung der Schaltungen erhält man an einigen Stellen Hinweise auf Gesetze der Digitaltechnik.
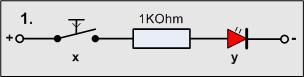
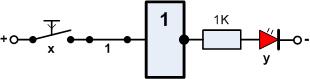
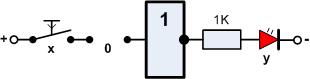
Versuch1
Material-Liste
- 1 Taster
- 1 Widerstand 1KOhm
- 1 LED
Das Ergebnis der Schaltung ist natürlich logisch
- wenn der Taster betätigt wird, leuchtet die LED
- wenn der Taster nicht betätigt wird, leuchtet die LED auch nicht
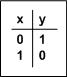
Wenn man mal die LED als Ergebnis y betrachtet, verhält sie sich genau wie der Schalter x! Man kann schreiben:
- y = x
Das Ergebnis ist logisch, stellt aber schon das Prinzip der Digitaltechnik dar:
-
zwischen 0 Volt und der Betriebsspannung 9 Volt gibt es keine Zwischenstufen!
0 Volt erhält die Bezeichnung 0; 9 Volt die Bezeichnung 1 - man schaltet nur zwischen 0 und 1 um!
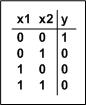
Den Sachverhalt kann man auch in Form einer kleinen Tabelle beschreiben, sie hat die Bezeichnung Wahrheitstabelle:
-
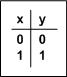
(Taster betätigt = 1; Taster nicht betätigt = 0)
-
LED's immer mittels Widerstand zuschalten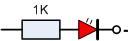

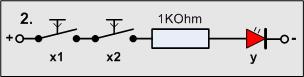
Versuch2
Material-Liste
- 2 Taster
- 1 Widerstände 1KOhm
- 1 LED
Wir schalten zum schon vorhandenen Taster einen weiteren in Reihe.
Das Ergebnis ist wieder ganz logisch:
- Die LED leuchtet nur dann, wenn beide Taster betätigt sind -
oder anders formuliert
nur wenn Taster x1 und x2 betätigt wird, leuchtet die LED - noch anders herum formuliert:
wenn nur ein Taster oder keiner betätigt wird, leuchtet die LED nicht
Das ist doch auch logisch, der Strom kann nur fließen wenn die Leitung keine Unterbrechung hat, also kein Taster offen ist, bzw. beide Taster geschlossen sind!
Das kann man wieder formulieren:
- y = x1 UND x2
Und nun die "digital technische" Beschreibung:
Wieder kann man eine Wahrheitstabelle aufschreiben:
-
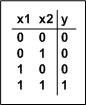
Für diesen logischen Sachverhalt AND
gibt es auch Schaltsymbole,
wir wollen das folgende verwenden: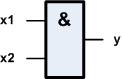
Versuch2a
Schalte den dritten Taster in Reihe mit x1 und x2.
- Formuliere den Sachverhalt als Formel (wie oben die "digital technische Beschreibung")!
- Schreibe eine Wahrheitstabelle auf!
- Wie sieht wohl das Schaltsymbol aus?
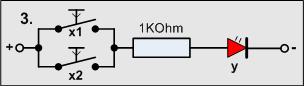
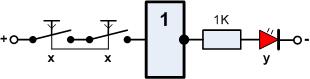
Versuch3
Material-Liste
- 2 Taster
- 1 Widerstand 1KOhm
- 1 LED
Jetzt werden die beiden Taster parallel geschaltet.
Man braucht nur einen Taster betätigen, welcher ist egal - auch beide, schon leuchtet die LED.
Wir finden dafür wieder eine logische Beschreibung:
- Die LED leuchtet wenn entweder Taster x1 oder x2 betätigt wird.
Das kann man wieder formulieren:
- y = x1 ODER x2
Und nun die "digital technische" Beschreibung:
Wieder kann man eine Wahrheitstabelle aufschreiben:
-
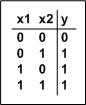
Das logische Schaltsymbol für OR
sieht wie fogt aus: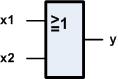
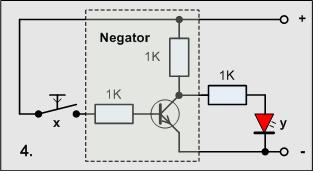
Versuch4
Material-Liste
- 1 Taster
- 3 Widerstände 1KOhm
- 1 Transistor
- 1 LED
Wenn alles richtig zusammen gesteckt ist, sollte bei Zuschalten der Betriebsspannung die LED sofort leuchten. Betätigt man nun den Schalter und die LED verlischt, dann haben wir alles richtig gemacht!
Wie funktioniert das?
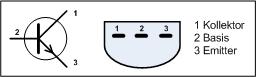
Der Transistor ist ein npn-Transistor, das bedeutet, das bei positiver Ansteuerung der Basis die Kollektor-Emitter-Strecke einen sehr kleinen Widerstand hat, bei Nichtansteuerung dagegen einen sehr großen.
Bei unserer Schaltung bedeutet das, dass bei offenem Taster die Kollektor-Emitter-Strecke einen Widerstand von etwa 1KOhm hat. Nach Spannungsteilerregel stellt sich die Spannung proportional zu den Widerständen ein, bedeutet, dass in diesem Fall etwa die halbe Betriebsspannung über den Transistor abfällt. Macht man den Kollektorwiderstand kleiner, wird die Spannung am Kollektor größer - aber Vorsicht, der Transistor verträgt nur einen bestimmten Strom. Bei z.B. 10V Betreibsspannung fließt ein maximaler Strom von 10mA, dass muss man mit dem Datenblatt des Transistors vergleichen, der Wert muss größer sein.
(der Transistor BC 548 verträgt einen maximalen Kollektorstrom von 100mA, d.b. man könnte den Kollektorwiderstand noch auf 100Ohm reduzieren)
Bezeichnung der Transistor-Beine:
Wird der Taster nun geschlossen, also eine positive Spannung an die Basis gelegt, wird der Widerstand der Kollektor-Emitter-Strecke sehr klein, am Kollektor mißt man nun fast keine Spannung (etwa 0,01V), man sagt, der Punkt wird auf Masse gelegt.
Damit ergibt sich nun folgendes Verhalten der Schaltung:
- Taster auf - LED leuchtet, Taster zu - LED aus
Das Ausgangssignal verhält sich genau entgegengesetzt zum Taster
In der Digitaltechnik bezeichnet man das als
- Negation
und man schreibt:
-
y = NICHT x ( y = NOT x ) oder auch 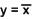
Auch hier für gibt es eine Wahrheitstabelle:
-
Das logische Schaltsymbol für die Negation
sieht wie fogt aus: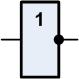
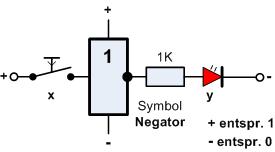
In den weiteren Schaltungen taucht dieses Symbol immer wieder auf, dann soll die oben im gestrichelt umrandeten Kästchen dargestellte Schaltung (ein Transistor, zwei Widerstände) aufgebaut werden!
Die Schaltung4 hätte damit folgendes Aussehen:
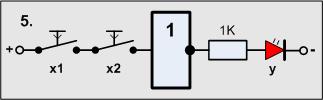
Versuch5
Material-Liste
- 2 Taster
- 1 Widerstand 1KOhm
- 1 LED
- 1 Negator (1 Transistor, 2 Widerstände)
Beide Taster werden nun wieder in Reihe geschaltet.
Folgendes Ergebnis kann man feststellen:
- Die LED leuchtet nur dann nicht wenn beide Taster betätigt werden -
oder anders formuliert
nur wenn Taster x1 und x2 betätigt wird, leuchtet die LED nicht - noch anders herum formuliert:
wenn ein oder kein Taster betätigt wird, leuchtet die LED
Man kann es sich so merken:
Zunächst wird das logische Ergebnis der Taster erzeugt und dann für die Ausgabe negiert
- y = (x1 UND x2) => negiert
z.B.
1 UND 0 = 0 => negiert = 1
oder
1 UND 1 = 1 => negiert = 0
Und nun die "digital technische" Beschreibung:
-
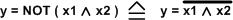
y = NAND ( x1, x2 )
Wieder kann man eine Wahrheitstabelle aufschreiben:
-
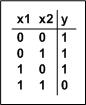
Für diesen logischen Sachverhalt NAND
wollen wir das Schaltsymbol verwenden: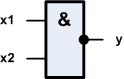
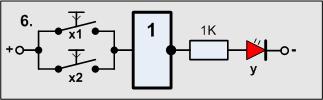
Versuch6
Material-Liste
- 2 Taster
- 1 Widerstand 1KOhm
- 1 LED
- 1 Negator (1 Transistor, 2 Widerstände)
Beide Taster werden nun aber parallel geschaltet, gefolgt vom Negator.
Folgendes Ergebnis kann man feststellen:
- Die LED leuchtet nur dann wenn kein Taster betätigt wird
- anders herum formuliert:
wenn ein oder beide Taster betätigt werden, leuchtet die LED nicht
Man kann es sich wieder so merken:
Zunächst wird das logische Ergebnis der Taster erzeugt und dann für die Ausgabe negiert
- y = (x1 ODER x2) => negiert
z.B.
1 ODER 0 = 1 => negiert = 0
oder
0 ODER 0 = 0 => negiert = 1
Und nun die "digital technische" Beschreibung:
-
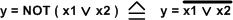
y = NOR ( x1, x2 )
Wieder kann man eine Wahrheitstabelle aufschreiben:
-
Für diesen logischen Sachverhalt NOR
wollen wir das Schaltsymbol verwenden: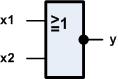
Beschreibung des Schaltkreises 4011
So - das waren nun die wichtigsten Grundelemente der Digitaltechnik!
Das funktioniert sehr gut, jedoch sind die Eingänge die Taster. Will man mehrere
solche Grundelemente miteinander verschalten, dann sind die Taster hinderlich, denn
wir brauchen Schaltungen, in denen die "Taster von außen gesteuert" werden. Das geht
natürlich sicher so in der Art wie unser Negator, denn wird der Transistor angesteuert
wird sein Kollektor-Emitter-Widerstand sehr klein, also so wie als wenn ein Schalter
geschlossen wird. So wird das auch realisiert, aber eben besser und mit einer anderen
Art von Transistoren, mit sogenannten MOS-FET-Transistoren.
Die Industrie hat das schon lange erkannt und entsprechende Bauelemente bereitgestellt.
Ein solcher Baustein ist z.B. der 4011
Da die Schaltung, obwohl natürlich umfangreicher als unsere Versuche, ist die
Schaltung zur Realisierung einer digitalen Grundfunktion recht klein. Deshalb sind
meist mehrere gleiche Grundfunktionen auf einem Baustein integriert.
In dem Baustein 4011 geht es um die Grundfunktion NAND und das gleich 4 mal:
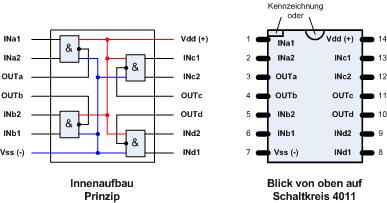
Da nun 4 x 2 Eingänge, 4 x 1 Ausgang, 1 x Plus(+ (Vdd)) und 1 x Minus (- (Vss))
bereitgestellt werden müssen, hat der Baustein 14 Beine (rechtes Bild). Das linke
Bild zeigt wo die Drähte nach außen geführt werden.
Die Daten des Bausteines wollen wir nicht in den Vordergrund stellen, nur so viel:
Die Betriebsspannung kann 5 bis etwa 15V betragen, das ist sehr gut.
Es gibt aber ein paar Dinge, die man niemals tun sollte:
|

|
Alle genannten Aktionen führen in der Regel zur Zerstörung des Schaltkreises!
Unabhängig von den eben genannten Fehlschaltungen, stehen uns nun gleich 4 NAND-Gatter zur Verfügung - damit wollen wir nun jede Menge neue Schaltungen probieren
los gehts - viel Spaß
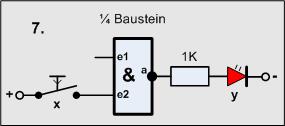
Versuch7
Material-Liste
- 1 Taster
- 1 Widerstand 1KOhm
- 1 LED
- 1 4011 (1 Gatter)
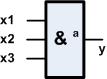
(Als Gatter wird eine logische Einheit auf einem Schaltkreis bezeichnet)
Wir stecken die Schaltung mit einem beliebigen Gatter des Schaltkreises zusammen -
kontrollieren - Betriebsspannung einschalten
und was sehen wir?
Man kann den Taster betätigen oder nicht es funktioniert alles nicht so richtig.
Interessant ist, wenn man einmal die Beine des (benutzten) Gatters mit den Fingern
berührt - die LED leuchtet mit unterschiedlicher Helligkeit, es geht, manchmal aber
nicht.
Der wissensdurstige Bastler wird sich sofort fragen - warum ist das so?
- ist die Schaltung falsch?
- habe ich einen Fehler gemacht?
- ist der Schaltkreis kaputt?
Keine Sorge, es ist alles richtig, wir haben ein grundlegendes Gesetz der praktischen digitalen Schaltungstechnik entdeckt:
-
Alle Eingänge eines Gatters müssen immer beschaltet werden,
offene Eingänge verfälschen das Ergebnis!
Die digitale Schaltungstechnik hat dafür Lösungen parat. Diese wollen wir mit der nächsten Schaltung im Versuch8 kennen lernen.
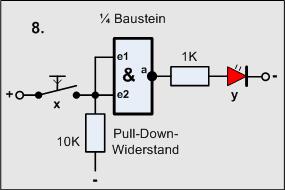
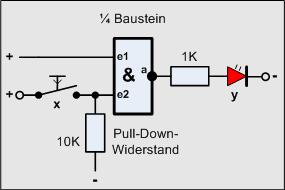
Versuch8
Material-Liste
- 1 Taster
- 1 Widerstand 1KOhm
- 1 Widerstand 10KOhm
- 1 LED
- 1 4011 (1 Gatter)
Nach Einschalten der Betriebsspannung sollte die LED nun stabil leuchten.
Betätigt man den Taster geht die LED aus.
1. Feststellung:
- Die Schaltung funktioniert wie ein Negator
Die beiden Eingänge des Gatters fungieren so wie die Steuerung jeweils eines Tasters. Wir haben nun beide Eingänge parallel geschaltet. Man könnte sagen, dass die Taster (intern) in Reihe geschaltet sind und immer zur gleichen Zeit betätigt werden, wie so ein zweipoliger Schalter. Folgendes Bild soll das auch erklären:
Da beide Taster immer zur gleichen Zeit betätigt werden, kann man das gleiche
Ergebnis auch mit einem Taster erreichen.
2.Feststellung:
-
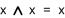
Eingänge dürfen parallel geschaltet werden!
Nutzt man das in unserem Fall zur Beschreibung:
Die Formel sagt, dass es sich um einen klassischen Negator handelt.
Aber wir haben ein Problem noch nicht gelöst, beide Eingänge sind zwar zusammen geschaltet,
aber einen definierten Pegel haben sie nicht - es funktioniert schlecht.
Unsere Schaltung zeigt, dass man das durch einen Widerstand realisieren kann.
Das passiert:
Die Gattereingänge werden schon mit sehr kleinen Strömen gesteuert, d.b. über den
Widerstand 10k fließt nur ein äußerst geringer Strom. Da nach dem Ohmschen Gesetz
U = I x R sich die Spannung proportional zum Strom verhält, gibt es auch nur einen
geringen Spannungsabfall über den 10k Widerstand, man sagt:
-
der Eingang wird durch den Widerstand auf Masse gelegt
oder
der Pegel des Eingangs wird auf Masse herunter gezogen
daher die englische Bezeichnung "Pull-Down-Widerstand"
Wird nun der Taster betätigt, bildet die Leitung vom Taster und der 10k Widerstand
einen Spannungsteiler. Die Spannung verhält sich wieder proportional zu den
Widerständen, also fällt über 10K nachezu die gesamte Spannung ab,
am Eingang liegt die Betriebsspannung, also 1.
Der Strom durch den Widerstand beträgt bei 10V nur 1mA, das ist akzeptabel.
3. Feststellung:
- Mit einem Pulldownwiderstand wird der Eingangspegel definiert auf 0 gelegt!
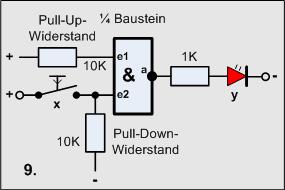
Versuch9
Da haben wir eben gelernt, dass man zwei gekoppelte Taster durch einen ersetzen kann.
Da stellt sich denn die Frage wie man von den gekoppelten Tastern einen beseitigen
kann - ganz einfach, man überbrückt ihn mit einem Draht. Überbrücken heißt,
der Schalter ist ständig zu, beschrieben durch eine 1. Aus dem Versuch5 wird dann
folgende Anordnung:
Jetzt muß man versuchen beim Gatter einen Eingang auf 1 zu legen den anderen auf den Taster. Das ist dann unserer nächster Versuch:
Material-Liste
- 1 Taster
- 1 Widerstand 1KOhm
- 2(1) Widerstände 10KOhm
- 1 LED
- 1 4011 (1 Gatter)
Der untere Eingang wird genauso wie eben beschaltet, der obere wird über einen
Widerstand an Betriebsspannung auf 1 gelegt. Der Pegel wird nun nach oben gelegt,
er hat die Bezeichnung Pull-Up-Widerstand.
Da aber dieser Eigang nicht zusätzlich über einen Taster gesteuert werden soll,
kann er auch gleich ohne Widerstand an + Betriebsspannung, also 1 gelegt werden:
Die Funktion entspricht wieder genau dem Negator.
Für die Reihenschaltung der "beiden Taster" kann man folgendes formulieren:
Für den Negator gilt dann:
Also beide Arten zur Beschaltung eines NAND-Gatters mit zwei Eingängen zum Negator sind möglich.
Frage:
- Wie müßte die Beschaltung eines NAND-Gatters mit 4 Eingängen aussehen, wenn es zum Negator umfunktioniert werden soll?
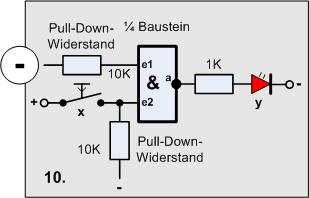
Versuch10
Material-Liste
- 1 Taster
- 1 Widerstand 1KOhm
- 2(1) Widerstände 10KOhm
- 1 LED
- 1 4011 (1 Gatter)
Im Unterschied zur vorhergehenden Schaltung wird der obere Eingang des Gatters auf
- Betriebsspannung, also 0, gelegt. Das kann schnell mal pssieren beim Beschalten,
die Wirkung ist jedoch erstaunlich:
- Man kann den Taster betätigen - es passiert nichts mehr, die LED ist immer an!
In solchen Fällen muss man noch einmal genau kontrollieren, das Gatter ist nicht kaputt, es ist ein Schaltungsfehler, denn die ganze Schaltung kann man einsparen und gleich eine 1 auf das vielleicht folgende Element legen. Folgende Ersatzschaltung mit Taster kann man finden:
Wir haben also einen Taster und einen Leitungsbruch in Reihe geschaltet. Das da nichts raus kommt weiß jeder. Den Sachverhalt kann man auch beschreiben:
Mit der Negation am Ende muß wohl 1 herauskommen:
Aufgabe:
Natürlich kann man wieder den Pulldownwiderstand am oberen Eingang weglassen und
den Eingang direkt auf - Betriebsspannung, also 0, legen.
Probiere das auch einmal aus!
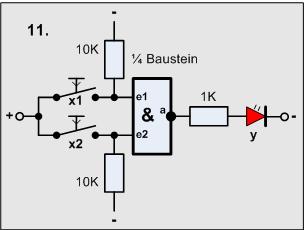
Versuch11
Material-Liste
- 2 Taster
- 1 Widerstand 1KOhm
- 2 Widerstände 10KOhm
- 1 LED
- 1 4011 (1 Gatter)
Das ist eine klassische NAND-Schaltung mit 2 Eingängen.
Aufgabe:
Baue die Schaltung auf und vergleiche die Wahrheitstabelle mit der vom Versuch5!
Versuch12
Ein paar Gesetzmäßigkeiten der Digitaltechnik haben wir schon kennengelernt.
Nun wollen wir aber weitere ganz tolle Eigenschaften mittels weiterer kleiner
Versuche herleiten.
Es ist kaum zu glauben, aber mit negierenden Gattern wie NAND's oder NOR's
kann man alle logischen Funktionen realisieren. Allerdings brauchen wir dazu
mehrere Gatter und wir wollen das ausschließlich mit NAND's probieren.
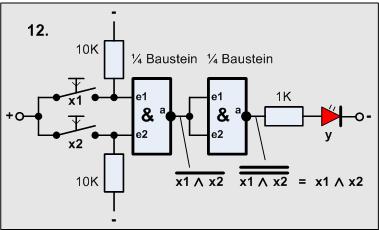
Als erstes wollen wir aus NAND's eine AND-Schaltung erzeugen:
Material-Liste
- 2 Taster
- 2 Widerstände 10KOhm
- 1 Widerstand 1KOhm
- 1 LED
- 1 4011 (2 Gatter)
Wir schalten an den Ausgang des NAND's ein zum Negator gestaltetes weiteres NAND.
Am Ausgang hinter dem erste Gatter verhält sich das Signal nach der aus Versuch5
bekannten Funktion:
Das Signal, beschrieben durch die Funktion wird noch einmal negiert, heißt, es wird ein weiterer Strich über die Funktion geschrieben:
Und man sieht schon das Ergebnis, es entsteht eine UND-Funktion, also werden beide Striche beseitigt. Dies aufgeschrieben:
Mit Worten
- Die Negation der Negation hebt sich auf!
Aufgabe:
Baue die Schaltung auf und vergleiche die Wahrheitstabelle mit der vom Versuch2!
Versuch13
Nun wirds spannend,
wir wollen aus NAND's eine ODER-Funktion aufbauen? Noch ein
weiteres Gatter wird nun gebraucht.
Wir wollen zunächst die Schaltung aufbauen und probieren und im Anschluß auch den
Nachweis per Formel erbringen.
Material-Liste
- 2 Taster
- 2 Widerstände 10KOhm
- 1 Widerstand 1KOhm
- 1 LED
- 1 4011 (3 Gatter)
Zunächst werden beide Eingangssignale durch jeweils ein entsprechend beschaltetes
NAND-Gatter negiert.
Die negierten Signale werden im folgenden NAND-Gatter mit der NAND-Funktion
verknüpft. Das Ergebnis steht als Formel da, hat aber nichts mit ODER zu tun - oder?
Wenn man das jedoch weiter umwandelt entsteht Folgendes:
Nach dem ersten = ist der lange Strich weg, jedes x wird einzeln negiert, aber das
Rechenzeichen wandelt sich von "und" in "oder".
Im nächsten Schritt kann jeweils die doppelte Negation weggelassen werden und schon
steht da x1 oder x2 - ob das stimmt, mann kann es ja probieren.
Wir wollen das noch einmal aufschreiben:
Mit Worten
- Wird die Negation über zwei Werte aufgehoben, so wird jeder einzelne Wert negiert und das Rechenzeichen kehrt sich um!
Aufgabe:
Baue die Schaltung auf und vergleiche die Wahrheitstabelle mit der vom Versuch3!
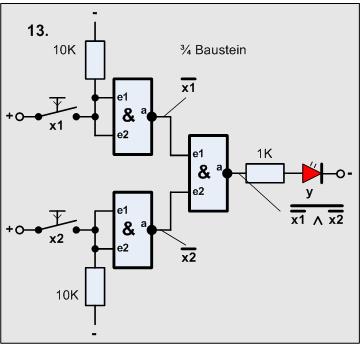
Versuch14
Diesmal gibt es keine Schaltung, sondern eine verbale Aufgabe.
Aufgabe:
Baue eine Schaltung zur Realisierung der NOR-Funktion auf und vergleiche die Meßergibnisse
mit der Wahrheitstabelle vom Versuch6!
Tip: Der Ausgang der Schaltung von Versuch13 muß einfach noch einmal negiert werden (wir haben noch ein Gatter auf dem Baustein).
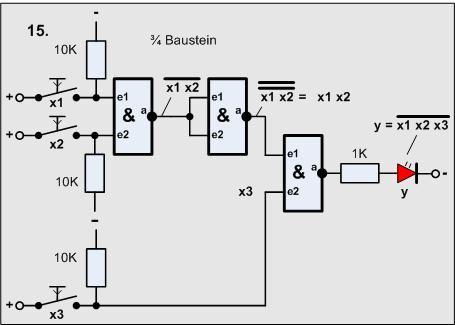
Versuch15
Jetzt folgt eine Aufgabe, die nicht ganz einfach ist, aber häufig in der Praxis gebraucht wird:
-
Es wird ein NAND-Gatter mit 3 Eingängen gebraucht.
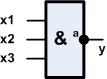
Dieses Gatter ist als Schaltung aus NAND-Gattern mit 2 Eingängen zu erzeugen.
Zunächst einmal wollen wir eine vereinfachte Schreibweise der UND-Funktion definieren:
Folgende Schaltung wäre denkbar:
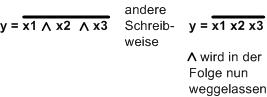
Mit unserem Wissensstand sieht man sofort, das geht nicht, denn wir brauchen 5 Gatter.
Aber man sieht auch, dass x3 zweimal hintereinander negiert wird, also können beide
gestrichen werden, x3 wird direkt benutzt. Und es werden nur noch 3 Gatter gebraucht.
Das ist auch ganz typisch für die Digitaltechnik, man sollte erst mal schauen,
vielleicht kann etwas vereinfacht werden, bevor der Aufbau der Schaltung beginnt.
Zum Vereinfachen stehen ebenfalls leistungsstarke Verfahren in der Technik bereit.
Nun die Schaltung:
Material-Liste
- 3 Taster
- 3 Widerstände 10KOhm
- 1 Widerstand 1KOhm
- 1 LED
- 1 4011 (3 Gatter)
Aufgabe:
Baue die Schaltung zur Realisierung der NAND3-Funktion auf und vergleiche die Meßergibnisse
mit der folgender Wahrheitstabelle:
Versuch16
Diesmal gibt es wieder keine Schaltung, sondern eine verbale Aufgabe.
Aufgabe:
Baue eine Schaltung zur Realisierung einer AND-Funktion mit 3 Eingaängen auf!
Tip: Im Versuch15 hatten wir eine NAND-Schaltung mit 3 Eingängen. Da wir noch ein Gatter frei haben, schalten wir das nur an den Ausgang der Schaltung von Versuch15.
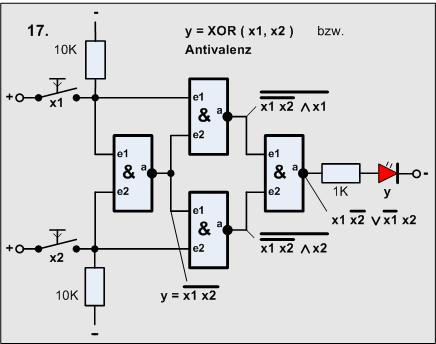
Versuch17
Material-Liste
- 2 Taster
- 2 Widerstände 10KOhm
- 1 Widerstand 1KOhm
- 1 LED
- 1 4011 (4 Gatter)
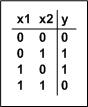
Die Schaltung hat die Bezeichnung XOR oder auch Antivalenz - wozu braucht
man so was?
Wir schauen uns einfach mal die Wahrheitstabelle an:
Immer wenn x1 und x2 unterschiedlich sind (einer 0 der andere 1) erscheint im Ergebnis eine 1, sind sie hingegen gleich, ist das Ergebnis 0.
Aber immer noch nicht ist deutlich, wo man es braucht - es ist ein Teil eines Computers,
es ist das minimalste Addierwerk, es gilt:
Die ersten drei Zeilen sind verständlich, nicht die vierte?
Wir denken in einem anderen Zahlensystem, dem Dualsystem, da gibt es nur die Zahlen 1 und 0, da kann 1 + 1 nun nicht 2 sein. Das ist genau wie im beim uns gebräuchlichen Dezimalsystem denn 1 + 9 ist 10, aber wir schreiben in der Einerstelle nur eine 0, 1 ist der Übertrag in die nächste Stelle.
Zum vollständigen Addierer muss der Übertrag auch noch erzeugt werden. Das geht mit unserem einen Baustein nicht mehr, aber wir haben schon so eine Schaltung. Hier einmal die Wahrheitstabelle der Schaltung:
Das war genau die AND-Funktion aus Versuch2.
Ein weiteres Problem gibt es noch, denn wir können so nur in einer Stelle rechnen,
die Einerstelle (die Bezeichnung ist im Dualsystem nicht ganz richtig). Wir müssen
auch den Übertrag von der vorhergehenden Stelle berücksichtigen, die Schaltung
wird logischerweise etwas größer.
Wir wollen die Schaltung nicht aufbauen, aber es ist einfach genial wie aus den
kleinen logischen Bauelementen die Grundelemente der Computertechnik entstehen!
Und noch etwas fällt kaum auf: "Man benutzt logische Bauelemente - realisiert damit
aber eine arithmertische Funktion!"
Man muss also zwischen AND (^ logisches UND) und
ADD ( + arithmetisches UND) unterscheiden!
Hinweis: Die logische Funktion Valenz kriegen wir auch noch hin, denn das ist nur die Negation der Antivalenz, schalten wir doch einfach unseren mit einem Transistor selbst gebauten Negator an den Ausgang der Antivalenz!
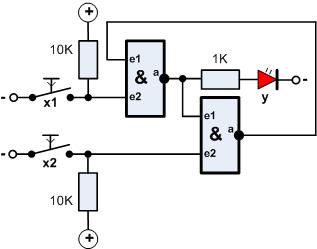
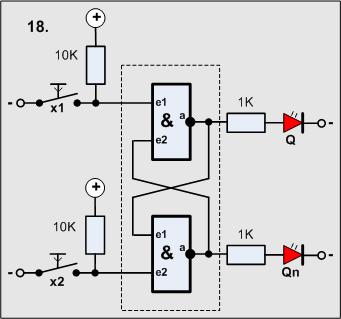
Versuch18

|
Von nun an wollen wir uns mit einer anderen Art der Zusammenschaltung von logischen
Bauelementen beschäftigen. Im Gegensatz zur bisherigen Strategie werden Ausgänge
der logischen Elemente auch wieder auf den Eingang zurück geführt - das gibt völlig
neue Effekte.
Fangen wir mal ganz langsam an |
Der Ausgang des zweiten NAND-Gatters wird wieder an den einen Eingang des ersten Gatters gelegt:
Man sollte auch an den Ausgang des zweiten Gatters eine LED plus Widerstand schalten, dann kann man besser die Funktion sehen.
Üblicherweise wird die Schaltung anders gezeichnet, die Funktion ändert sich deshalb aber nicht, es hat eine symbolische Wirkung:
Material-Liste
- 2 Taster
- 2 Widerstände 10KOhm
- 1(2) Widerstände 1KOhm
- 1(2) LED
- 1 4011 (2 Gatter)
Zu beachten ist, dass die Eingänge mit Pull-Up-Widerständen an 1 (+ Betriebsspannung) gelegt werden. Auf die Eingänge wird bei Betätigung der Taster eine 0 gelegt.
Was passiert, was sollte man nun sehen?
Wir schalten ein - es sollte eine LED leuchten.
Jetzt betätigen wir den Taster, an dem die LED nicht leuchtet - sofort leuchtet
auch die entsprechende LED, die andere geht aus.
jetzt läßt man den Taster los - es ändert sich nichts bei den LED's.
Betätigt man wieder den anderen Taster, tauschen sich die Verhältnisse aus.
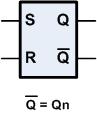
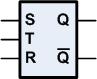
Da die Einstellungen auch bei offenem Taster bleiben, bezeichnet man die jeweilige Stellung als Zustand der Schaltung. Diese Schaltung wird als Latch (nach amerikanischen Sprachgebrauch) bezeichnet. Folgendes Symbol wird verwendet:
Die Eingänge haben die Bezeichnung R und S, die Ausgänge Q und Qn (Qn - Q negiert), das Gebilde heißt nun genauer RS-Latch.
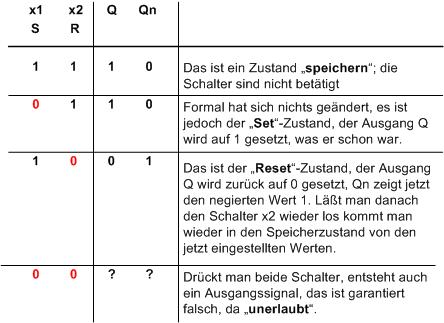
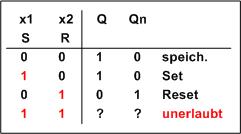
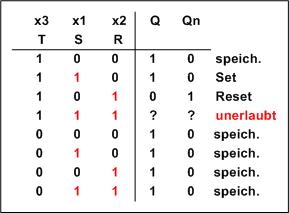
Die Wahrheitstabelle, die nun Zustandstabelle heißt, beschreibt Reaktion der Schaltung:
Und wieder haben wir eine der wichtigsten Grundschaltungen des Computers. Ein Latch behält seine Einstellung, wenn auch kein Signal zur Steuerung vorhanden ist, es speichert den Wert (Einstellung)!
Diese Anordnung kann also genau 1 Bit speichern.
Baut man 2 x 8 x 109 (also: 16 000 000 000 ) solcher Schaltungen auf, hätte man den ganz brauchbaren RAM-Hauptspeicher eines Computers von 2GByte (statisches RAM). Das macht man aber nicht, denn ein RAM-Speicher ist zu groß. Als Hauptspeicher nutzt man dynamische Speicher, die brauchen weniger Platz, der beschriebene Speicher wird im Cache genutzt, er ist sehr schnell.
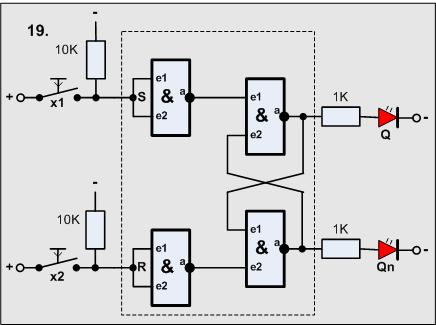
Versuch19
Die eben beschriebene Schaltung funktioniert sehr gut, jedoch entspricht ihre Steuerung nicht den Vorschriften. Diese lauten:
Es wird generell mit 1 geschaltet, sind hingegen beide Eingänge 0 wird gespeichert.
Das Problem läßt sich relativ einfach beheben, wir haben ja noch zwei Gatter frei, die schalten wir vor die Eingänge als Negator:
Material-Liste
- 2 Taster
- 2 Widerstände 10KOhm
- 2 Widerstände 1KOhm
- 2 LED
- 1 4011 (4 Gatter)
Für diese Anordnung dürfen wir nun erst das schon oben gezeigte Symbol für ein
RS-Latch verwenden.
Überprüfe, ob die Zustandstabelle erfüllt wird!
Anwendung:
Die wichtigste Anwendung ist wohl die als Cache im Computer, aber auch andere gibt es
z.B. Ein- Ausschalter;
Steuerung von Lichtsignalen auf Modellbahnen;
steuert man gleichzeitig ein Relais mit Q bzw. Qn (über einen Transistor-Verstärker),
kann auch eine Fahrstromabschaltung erfolgen .
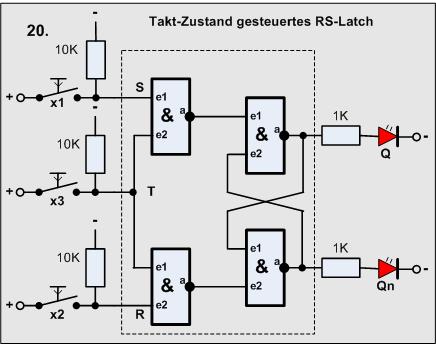
Versuch20
Nun eine weitere interessante und wichtige Schaltung:
Material-Liste
- 3 Taster
- 3 Widerstände 10KOhm
- 2 Widerstände 1KOhm
- 2 LED
- 1 4011 (4 Gatter)
Das Signal von x1 und x2 wird natürlich noch negiert, aber es geht nur wenn x3 ebenfalls betätigt wird, also eine 1 bereitgestellt wird, denn es gilt für die ersten Gatter:
- 1 UND 1 = 1 => negiert = 0 also wird das folgende Gater angesteuert.
Ist Taster x3 offen bleibt das Latch im Speicherzustand, denn:
-
xi UND 0 = 0 => negiert = 1 damit wird das folgende Gater nicht angesteuert.
(xi: i = 1, 2)
Wir haben für diese Anordnung ein neues Symbol mit folgender Zustandstabelle:
Die Schaltung heißt: Taktzustand gesteuertes RS-Latch
Anwendung:
Diese Schaltung ist wichtig in der Rechentechnik, es wird beim Speichern
erst das Einschwingen der Datenleitungen abgewartet, dann durch T = 1 die
Übernahme in den Speicher vollzogen.
Auch in anderen Schaltkreisen, wie beispielsweise Schieberegister oder Decoder
wird ähnlich verfahren. Das Signal heißt zumeist dann "Strobe".
Bei der Eisenbahn braucht man das auch:
Ist eine Fahrstraße durch den Bahnhof durch Stellen der Weichen festgelegt, wird
das Signal auf Fahrt gestellt. Jetzt darf man natürlich keine Weiche mehr verändern.
Jede Weiche hat so eine Schaltung, wird das Signal gestellt, wird an allen T-Eingängen
eine 0 gelegt und nichts geht mehr!
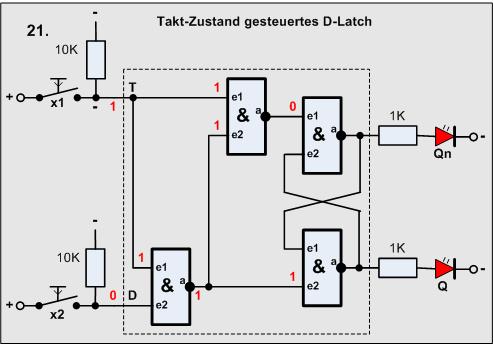
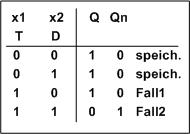
Versuch21
Der eben angedeutete Weg, die Ansteuerung des Latch zu verändern, ist ein
gebräuchlicher Weg, neue Kippglieder (so heißen sie ganz allgemein) zu erzeugen.
Da stehen für die Neugestaltung noch jede Menge Möglichkeiten offen -
hoffentlich werden die auch gebraucht?!
Nun also eine wieder veränderte Ansteuerung des Latch:
Material-Liste
- 2 Taster
- 2 Widerstände 10KOhm
- 2 Widerstände 1KOhm
- 2 LED
- 1 4011 (4 Gatter)
Den oberen Taster könnte man wieder als das Taktsignal bezeichnen (Verriegelung),
der untere ist der zu speichende Wert, also nur 0 oder 1. Der Wert wird nur
übernommen wenn x1 geschlossen ist.
Die roten Zahlen sollen das Verhalten der Schaltung für x2 = 0 und T (x1) = 1
zeigen.
-
Am unteren Gater entsteht damit: 1 (x1) UND 0 (x2) = 0 negiert 1.
Damit kann der untere Eingang des Latch nicht verändert werden.
Was passiert oben?
Der Takt ist 1 und von unten kommt ebenfalls eine 1 also:
-
1 UND 1 = 1 negiert 0
also wird der obere Eingang des Latch geschaltet. Am Ausgang entsteht eine 1.
Da haben wir ein Problem, denn eigentlich entspricht diese Ansteuerung dem Reset-Fall, dann muss unten eine 1 entstehen. Das Problem beheben wir ganz einfach durch Vertauschen der Ausgangsleitungen bzw. der Beschriftung, deswegen oben Qn.
Den Sachverhalt kann man wie bisher auch durch eine Zustandstabelle beschreiben:
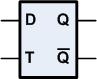
Diese Schaltung wird als Taktzustands gesteuertes D-Latch bezeichnet und hat das folgende SymboL:
Anwendung:
Dieses Latch wird auch zum Speichern genutzt.
Es hat den großen Vorteil, dass es keine unerlaubten Belegungen der Eingangssignale gibt!
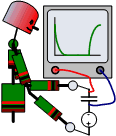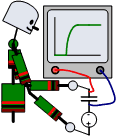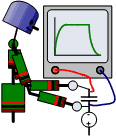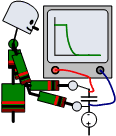
|
Versuch22 |
Jetzt beginnt wieder eine neue Art von Kippgliedern, Basis dazu ist das veränderte Taktsignal.
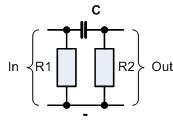
Die veränderte Schaltung am Takteingang wird als Hochpaß bezeichnet.
-
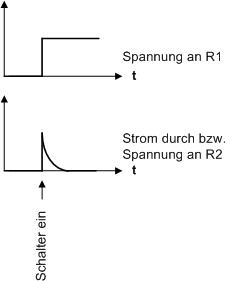
Wird eine 1 angelegt (In), fällt die Spannung über R1 etwas ab. Der Kondensator wird über R2 aufgeladen, so dass das proportionale Signal zum Strom an R2 zur Verfügung steht. Da der Strom nur ganz kurz den maximalen Wert annimmt und danach rasch auf 0 zurückgeht, entsteht ein Nadelimpuls für den Takteingang.
Das nun aufzubauende Kippglied sieht wie folgt aus:
Material-Liste
- 3 Taster
- 2 Widerstände 10KOhm
- 1 Widerstand 75KOhm
- 1 Widerstand 15KOhm
- 1 Elko 4,7uF
- 2 Widerstände 1KOhm
- 2 LED
- 1 4011 (4 Gatter)
Da für die Gatter nun nur noch einen kleinen Augenblick lang eine 1 bereitgestellt wird, wird nur für diese kleine Zeit der Zustand des Latch verändert. Man sagt, dass die Schaltung mit positiver Flanke gesteuert wird. Für diese Schaltung gibt es eine neue Bezeichnung:
- Flip-Flop
und ein neues Symbol:
Der Zeitpunkt der Umschaltung kann nun ganz genau festgelegt werden.
Das Ding hätte die Bezeichnung:
- RS-Flip-Flop, gesteuert mit ansteigender Flanke
Hätte - weil es dieses Kippglied kaum gibt.
Die Erzeugung des Nadelimpulses ist in der angegenen Schaltung schlecht, es funktioniert unzuverlässig. Die Industriellen Flip-Flop's brauchen viel mehr Gatter, die haben wir aber nicht!
Zur Kontrolle kann man am Punkt C eine weitere LED (über einen Widerstand von 1K) anschließen, diese blitzt bei Betätigung von x3 minimal auf.
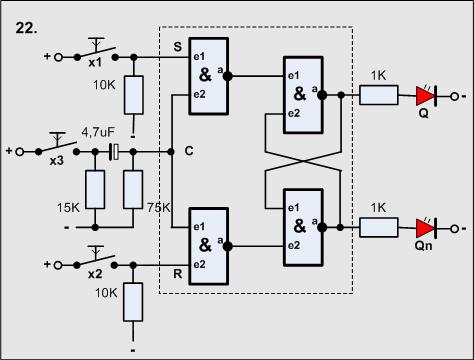
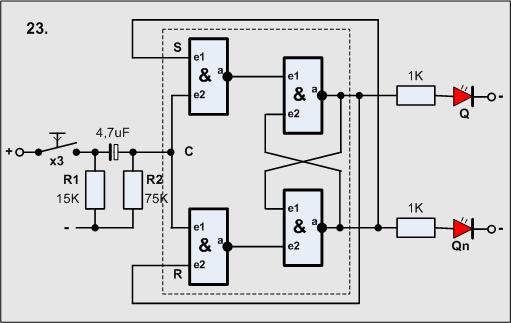
Versuch23
Wieder eine interessante Schaltung nur durch Veränderung der Beschaltung:
Material-Liste
- 1 Taster
- 1 Widerstand 75KOhm
- 1 Widerstand 15KOhm
- 1 Elko 4,7uF
- 2 Widerstände 1KOhm
- 2 LED
- 1 4011 (4 Gatter)
Interessant ist, dass die Ausgänge überkreuz an die Eigänge gelegt werden.
Hat man an Qn eine 1 so liegt diese auch am oberen Gatter. Kommt nun die kurze 1
vom Taktglied, so wird oben eine 0 erzeugt und das Latch geschaltet. An Q gibt es
nun eine 1. Würde nun noch die 1 vom Taktglied anliegen, würde das Latch sofort
zurück kippen, und wieder hin, und wieder her usw.
Der Taktimpuls muß kürzer als die Schaltzeit des Gatters sein, sonst funktioniert
das Ding nicht.
Das Ausgangssignal steht ab 40ns (Nanosekunden - 10-9sec -
0.000 000 000sec x 40 = 0.000 000 04sec) entsprechend der angelegten
Eingangssignale bereit - so schnell kann man nicht den Finger vom Taster lassen!
Unser Taktimpuls ist breiter, man müßte R2 und C viel kleiner machen
(Tau = R2 x C etwa= 0,04sec), dann geht es
aber auch nicht mehr, hier muß man also mehr Aufwand betreiben!
Richtig gut funktioniert das mit einem speziellen Baustein dem 4027, dass ist ein
JK-Flip-Flop.
Anwendung:
In Kombination mit Relais als Lichtschalter.
Hinweis:
Man kann aber diese "schlechte" Eigenschaft bewußt nutzen, denn wenn eine Schaltung
ständig hin und her kippt, kann man sie als Generator nutzen. Wir müssen sie aber
"im Zaum" halten, damit wir eine definierte Schwingung bekommen.
Das ist das Ziel der folgenden Schaltungen.
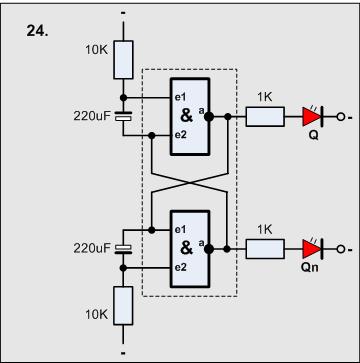
Versuch24
Material-Liste
- 2 Widerstände 10KOhm
- 2 Elko's 220uF
- 2 Widerstände 1KOhm
- 2 LED
- 1 4011 (2 Gatter)
Die Schaltung unterscheidet sich vom RS-Latch nur wenig.
Der zweite Eingang der Gatter wird
über einen Kondensator gesteuert, der seinerseits über einen Widerstand entladen
wird. Umgeschaltet wird nur dann, wenn mindest ein Eingang auf 0 liegen. Hat der
Ausgang unten eine 1, so sind beide Seiten des Kondensators 1. Langsam wird der
Kondensator entladen, kommt er zum 0-Pegel, erschein am Ausgang oben
eine 1 (0 und 1 = 0 negiert 1), der andere Kondensator wird aufgeladen usw.
Die Schaltung blinkt mit etwa 2Hz.
Werden die Kondensatoren und die Widerstände verkleinert, schwingt die Schaltung
mit höherer Frequenz. Ab einer bestimmten Frequenz kann man die Schwingungen hören –
wir haben einen Tongenerator mit Rechecksignal.
Die Schaltung hat die Bezeichnung:
- A-Stabiler Multivibrator
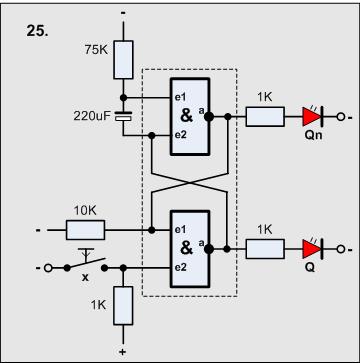
Versuch25
Material-Liste
- 1 Widerstand 10KOhm
- 1 Widerstand 75KOhm
- 1 Elko 220uF
- 3 Widerstände 1KOhm
- 2 LED
- 1 4011 (2 Gatter)
Bei Betätigung des Schalters kippt die Schaltung in den anderen Zustand.
Mit Entladung des Kondensators kippt die Schaltung nach einer gewissen Zeit,
bestimmt durch den Kondensator und den Widerstand 75K wieder in den Ausgangszustand
zurück und bleibt in diesem Zustand.
Nach etwa 6sec ist wieder der Ausgangszustand erreicht.
Grundzustand:
Ausg. oben 1, unten 0
Eing. unten 1 und 1 (1 und 1 = 1 negiert 0)
Schalter:
unten 1 und 0 = 0 negiert 1
Eing. oben beide 1, Ausg. 0, der oberste wird über den Widerstand langsam 0
(0 und 1 = 0 negiert 1) Schaltung kippt zurück.
Die Schaltung hat die Bezeichnung:
- Mono-Stabiler Multivibrator
Anwendungen:
Nachlaufschaltung, Treppenlicht usw.
Aufgabe26/27
Bei der Durchführung der Versuchen haben wir ganz nebenbei Gesetze der Digitaltechnik
kennen gelernt, das hat auch die Bezeichnung Schaltalgebra.
Die stehen schon mal alle auf dem Bildschirmhintergrund.
Zwei davon haben wir nicht behandelt, das ist nun die folgende Aufgabe:
Weise anhand einer Schaltung mit dem Baustein 4011 nach, dass die folgenden Gesetze richtig sind:
Es darf nichts passieren, wenn der Taster betätigt wird!
Hier kann man eine Kurzfassung als pdf.Datei aufrufen.
Teil 3: RS-Flip-Flop