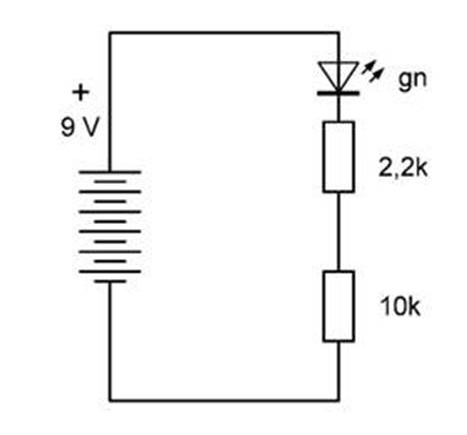
2.3 Mehr Widerstand

von Andreas Thaler

Elektronik-Labor Projekte Lernpakete Grundschaltungen

Zur Schaltung „Die LED im Stromkreis“ von Burkhard Kainka (Besprechung siehe hier) kommt jetzt ein 10-Kiloohm-Widerstand dazu, der in Reihe mit der LED und dem 2,2-Kiloohm-Widerstand liegt.

Das bedeutet, dass der Strom nun insgesamt ein größeres Hindernis zu überwinden hat, das aus der LED und den beiden Widerständen gebildet wird. Da jedoch die dafür zur Verfügung stehende Spannung (Kraft) mit 9 Volt gleich bleibt, wird die Stromstärke durch den zusätzlichen 10-Kiloohm-Widerstand verringert. Das Ohm‘sche Gesetz zeigt den Zusammenhang:

U = R * I

I = U/R

Je größer der Widerstand R ist, desto kleiner wird der Strom I bei gegebener Spannung U.

Krumme Kurven, Simulation und Überlegungen

Dass Schaltungen mit LEDs als Halbleiter und ihrer „krummen Spannungs-/Stromkurve“ nur schwer zu berechnen sind, haben wir unter anderem hier besprochen. Daher sehen wir uns als nächsten Schritt die Schaltung gleich in der Simulation an. Aber bevor wir das machen, überlegen wir uns doch vorher kurz gemeinsam, was wir in etwa an Gesamtstrom und Spannungen in der Schaltung zu erwarten haben.

Tatsächlicher und idealer Strom durch die LED

Zunächst ist es interessant zu sehen, dass die LED mit ihren beiden kräftigen Vorwiderständen recht wenig Strom erhalten erhalten wird.

Das „recht wenig“ bezieht sich auf die 20 mA Stromstärke, die üblicher Weise für LEDs als Zielstrom in Datenblättern zu finden sind.

Mit der Formel zur Berechnung des Vorwiderstandes für eine LED bei gegebener Spannung und Zielstromstärke können wir für unsere Schaltung den Vorwiderstand berechnen, der für die LED ideal wäre. „Ideal“ bedeutet maximale Helligkeit bei geringstmöglicher Belastung. Damit haben wir einen Vergleich und bekommen auch ein Gefühl dafür, was eine LED so an Strom zum Leuchten braucht.

R_V = (U_E - U_F)/I_LED

Vorwiderstand = (Eingangsspannung - Vorwärtsspannung)/LED-Strom

Gegebene Eingangsspannung UE: 9 V
Zielstromstärke: 20 mA
Vorwärtsspannung U_F: 1,97 V (ermittelt mit dem Bauteiletester in einem anderen Versuch)

R_V = (9 V - 1,97 V)/0,02 A
R_V= 351,5 Ohm ~ 352 Ohm

352 Ohm wäre also der Wert für den Vorwiderstand, damit bei 9 Volt Eingangsspannung 20 mA durch LED und Vorwiderstand fließen und die LED somit „optimal strahlt“. Da wir in unserer Schaltung zwei Widerstände in Reihe geschaltet haben, können wir beide Widerstandswerte addieren und erhalten so den Ersatzwiderstand (= Gesamtwiderstand R_ges):

R_ges = 2200 Ohm + 10000 Ohm
R_ges = 12200 Ohm = 12,2 kOhm

Das heißt, dass wir vom Idealwert 352 Ohm ein ganz schönes Stück weit entfernt sind. Es wird daher spannend, ob bei dem zu erwartenden geringen Strom die LED überhaupt leuchten wird.

Spannungsverteilung in der Reihenschaltung

Die zweite Sache, die wir uns überlegen sollten, ist die Spannungsverteilung in der Reihenschaltung, die aus der LED plus zwei Vorwiderständen gebildet wird. Da in einer Reihenschaltung am größten Widerstand die meiste Spannung abfällt (die Spannung als Kraft muss dort mehr arbeiten, wo der größere Widerstand ist), sollte dieser Effekt am 10-Kiloohm-Widerstand zu beobachten sein. Der 2,2-Kiloohm-Widerstand ist ja kleiner und bei der LED gehen wir davon aus, dass sie am wenigsten Widerstand aufweist.

Warum sollte das so sein?

Bei einer Vorwärtsspannung von 1,97 Volt und einem Vorwiderstand von 352 Ohm lässt die LED bereits ihren Maximalstrom von 20 mA durch.
Das bedeutet einen Spannungsabfall von 1,97 Volt an der LED und einen Spannungsabfall von 7,03 Volt am 352-Ohm-Widerstand.
Wenn aber bereits am 352-Ohm-Widerstand eine deutlich höhere Spannung abfällt als an der LED, dann muss das umso mehr bei unserem 12,2-Kiloohm-Ersatzwiderstand der Fall sein (in einer Reihenschaltung fällt ja die meiste Spannung am größten Widerstand ab). Der Ersatzwiderstand setzt sich, wie schon gesagt, aus dem 2,2-Kiloohm- und dem 10-Kiloohmwiderstand zusammen.

Sehen wir uns das gleich in der Schaltungssimulation mit EveryCircuit an.

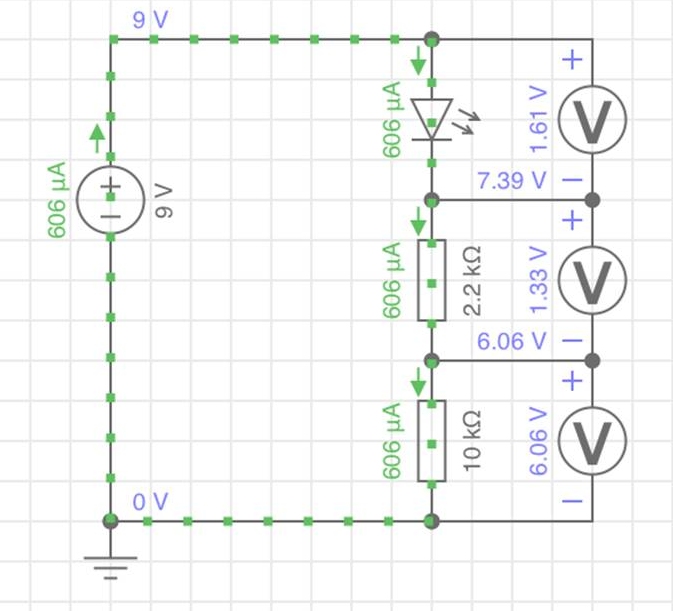
Hier das Bild für unsere aktuelle Schaltung:

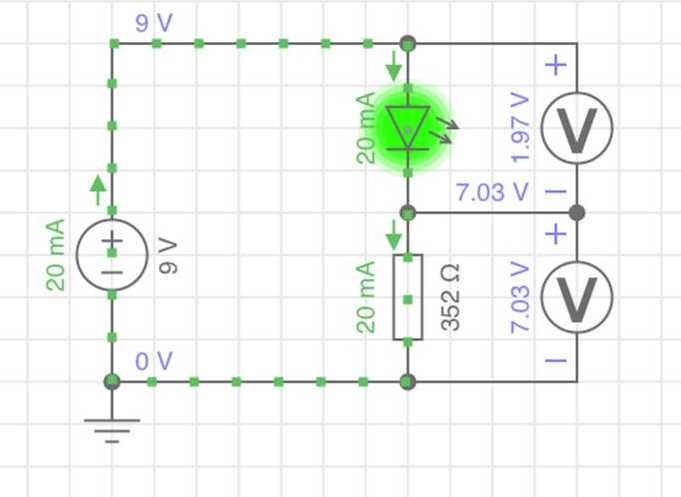
Und hier zum Vergleich das Bild für die Schaltung mit „idealem“ Vorwiderstand:

Wir sehen, dass

durch die LED mit beiden Widerständen ein Strom von 606 uA (= 0,606 mA) fließt und die LED - in der Simulation - nicht leuchtet;
am 10-Kiloohm-Widerstand wie erwartet die höchste Spannung abfällt und
die LED einen deutlich kleineren Vorwiderstand benötigt, um mit 20 mA happy und kräftig zu strahlen ;-)

Der Autor der Schaltung, Burkhard Kainka, verspricht uns jedoch, dass die LED leuchtet, wenn auch nur sehr schwach. Machen wir uns selbst ein Bild und bauen die Schaltung am Steckbrett auf.

Aufbau und Messung der Schaltung

Das ist am Steckbrett rasch gemacht. Die Anode der LED kommt an den Pluspol der stabilisierten Spannungsversorgung (Labornetzgerät), es folgen der 2,2-Kiloohm- und der 10-Kiloohmwiderstand, dessen Ausgang den Minuspol kontaktiert.

Und tatsächlich, die LED leuchtet! Wenn auch nur schwach, aber am Foto zu sehen. Messen wir jetzt mit dem Multimeter die Spannungsabfälle an der LED und den beiden Widerständen und stellen wir die Werte denen aus der Simulation gegenüber. Als Ergebnisse haben wir:

Bauteile	Spannungsabfälle gemessen (V)	Spannungsabfälle simuliert (V)
LED_grün	1,87	1,61
2,2k-Widerstand	1,29	1,33
10k-Widerstand	5,83	6,06

Alles im grünen Bereich, die Abweichungen tatsächliche Messerwerte zu simulierten Werten sind gering und daher in der Praxis zu vernachlässigen.

Der Gesamtstrom in der Schaltung

Wie sieht es mit dem Gesamtstrom aus, der durch die Reihenschaltung fließt?

Modus	Gesamtstrom (mA)
Messung	0,590
Simulation	0,606

Auch hier keine nennenswerte Unterschiede zwischen Messung und Simulation. Eine Differenz von 16 uA sollte man in der Praxis nicht bemerken bzw. ist das nur ein kleiner Unterschied in der Helligkeit der LED.

Und was ist mit der Bauteiletoleranz bei den Widerständen?

Jetzt wäre es noch interessant festzustellen, ob sich die Bauteiletoleranz von +/- 5 Prozent bei den Widerständen auf Spannungsabfälle und Gesamtstrom auswirkt. Mit dem Multimeter (Widerstandsmessung) messen wir für den 2,2-Kiloohm-Widerstand (Nennwert) tatsächliche 2,17 Kiloohm und für den 10-Kiloohm-Widerstand (Nennwert) tatsächliche 9,81 Kiloohm.Diese tatsächlichen Werte in die Simulation eingesetzt zeigt folgendes Bild:

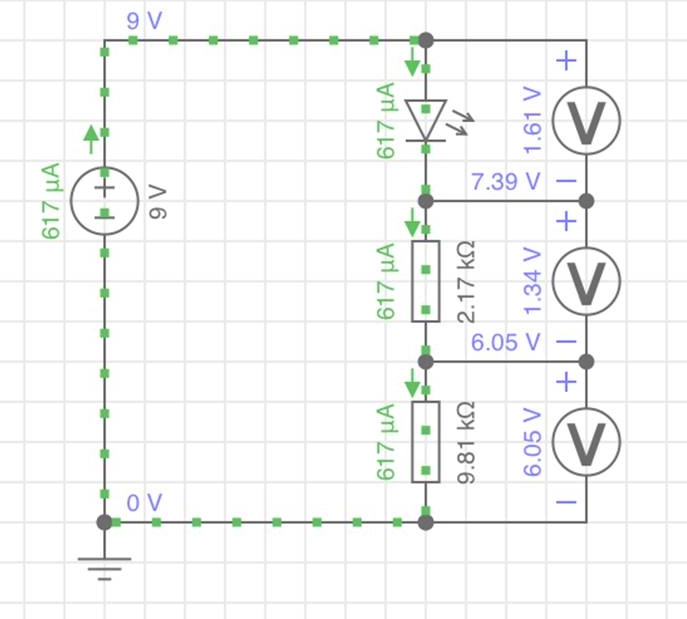
Auch hier sind die Abweichungen durch die Bauteiletoleranz nur minimal und damit für die Praxis zu vernachlässigen.

Zum Abschluss alle Werte in der Übersicht - gemessene Werte, Nennwerte simuliert und Spannungsabfälle tatsächliche Werte Widerstände simuliert:

Bauteile	Spannungsabfälle gemessen (V)	Spannungsabfälle simuliert (V)	Spannungsabfälle Simulation tatsächliche Widerstandswerte (V)
LED_grün	1,87	1,61	-
2,2k-Widerstand	1,29	1,33	1,34
10k-Widerstand	5,83	6,06	6,05

Gesamtströme in der Übersicht:

Modus	Gesamtströme (mA)
Messung	0,590
Simulation	0,606
Simulation mit tatsächlichen Widerstandswerten	0,617

Fazit

Es ist immer wieder erstaunlich, was man an einer - auf den ersten Blick - einfachen Schaltung alles beobachten kann. Dabei ist das hier nur Anwenderpraxis und keine theoretische Betrachtung auf Ebene der Halbleiterphysik und auch keine Netzwerkanalyse ;-)

Festzuhalten ist, dass mit Hilfe der Schaltungssimulation sehr präzise das Verhalten und die Werte einer Schaltung vorhergesagt werden können. Auch wenn in der realen Schaltung dann geringe Abweichungen auftreten, die man durch die Messung ermittelt, bewertet und gegebenfalls mit Bauteilen anderer Werte korrigiert.

Eine Schaltung vor dem Aufbau zu simulieren, verhindert auf jeden Fall überlastete Bauteile und mitunter auch verbrannte Finger ;-)