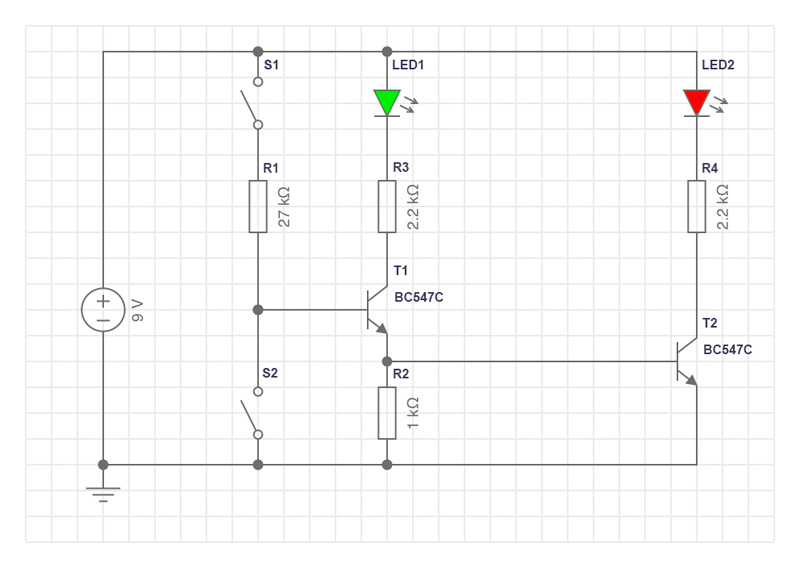
3.5 Gekoppelte Schalter

von Andreas Thaler

Elektronik-Labor Projekte Lernpakete Grundschaltungen

In dieser Schaltung von Burkhard Kainka arbeiten erstmals in dieser Versuchsreihe zwei Transistoren zusammen. Bei Schließen von S1 fließt Strom über die Basis-Emitter-Strecke von T1. Der Transistor schaltet durch, sein Kollektorstrom fließt durch die LED1 (grün), die LED leuchtet. Der Emitterstrom von T1 erzeugt an R2 (Emitterwiderstand) einen Spannungsabfall. Über die Emitterstrecke T1 - Basis T2 fließt Strom, T2 schaltet durch, sein Kollektorstrom fließt durch die LED2 (rot), die LED leuchtet. Schließt man zusätzlich S2, so wird die Basis-Emitterstrecke von T1 kurzgeschlossen. T1 sperrt da kein Basisstrom mehr fließt. Damit fließt auch kein Emitterstrom mehr durch R2, an R2 findet kein Spannungsabfall statt, T2 sperrt da ohne Basisstrom. Keine der LEDs leuchtet. Würde man in dieser Schaltung den Emitterwiderstand R2 weglassen, würde der Emitterstrom von T1 direkt nach Masse abfließen. Die Basis von T2 würde gemeinsam mit dem Emitter von T1 auf Massepotential liegen, damit liegt keine Spannung an der Basis von T2 an, T2 sperrt.

Berechnungen

Eine Handberechnung gestaltet sich durch die Zusammenschaltung der beiden Transistoren für den Praktiker bereits relativ anspruchsvoll, soll aber dennoch versucht werden. Es handelt sich bei den im Anschluss durchgeführten Berechnungen lediglich um eine Näherung, die anhand der Werte der anschließenden Schaltungssimulation und Messung überprüft wird.

Basistrom T1

Der Basisstrom von T1 fließt vom Pluspol der Spannungsquelle über R1, weiter über die Basis-Emitter-Strecke von T1, welche sich auf die Strecke Emitterwiderstand R2 – Masse sowie die Basis-Emitter-Strecke von T2 nach Masse aufteilt. Der Spannungsabfall an R2 ist unbekannt. Somit kann der Basisstrom von T1 (Reihenschaltung R1 – Basis-Emitterstrecke T1 nach R2 und T2) nicht berechnet werden. Das gilt auch für den Basisstrom von T2.

Bei voller Durchschaltung fallen an der Kollektor-Emitter-Strecke von T1 geschätzt ca. 0,1 Volt ab. Der Spannungsabfall an der LED1 (grün) beträgt geschätzt ca. 1,7 V.

Berechnung des maximalen Kollektorstroms T1 mit der Formel für den Vorwiderstand einer LED:

R_V= (U_E – U_F) / I_{C T1 max}

3,2 kOhm = (9,0 V – 1,7 V – 0,1 V) / I_{C
T1 max}

I_{C T1 max} = 7,2 V / 3,2 kOhm

I_{C T1 max} = 2,25 mA

Berechnung des maximalen Spannungsabfalls an R2 durch Einsetzen von I_{C T1 max}:

U = R * 1

U_{R2 max} = R2 * I_{CT1 max}

U_{R2 max} = 1 kOhm * 0,00225 A

U_{R2 max} = 2,25 V

Berechnung des Basisstroms T1:

I = U / R

I_{B T1}= (9,0 V – 0,7 V – 2,25 V) / 28 kOhm

I_{B T1} = 6,05 V / 28 kOhm

I_{B T1} ~ 216 uA

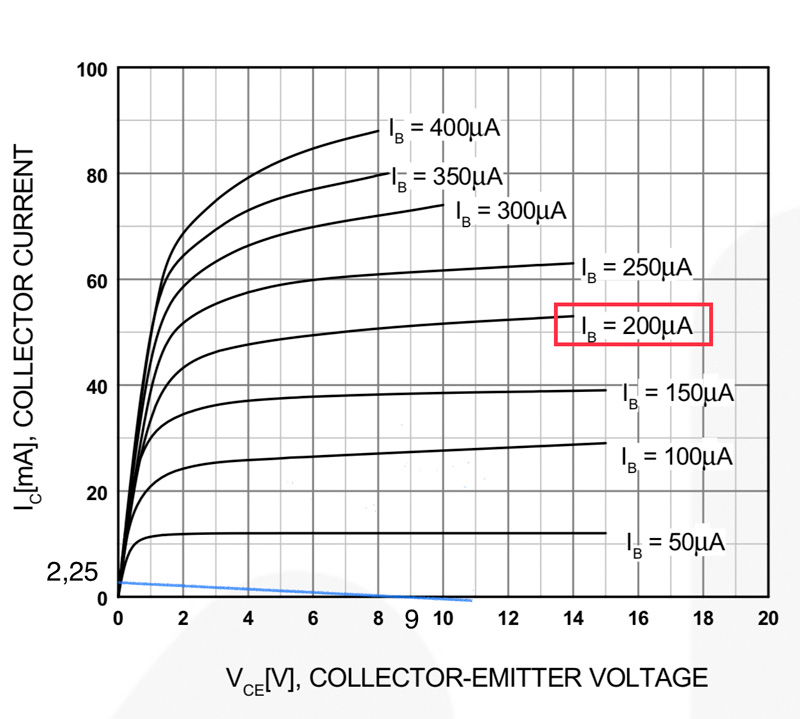
Das Kennlinienfeld zum Transistor BC547C zeigt, dass bei einer Widerstandsgeraden 2,25 mA : 9 V ein Basisstrom von ~ 200 uA den Transistor auf jeden Fall voll durchschaltet:

Für U_BE
T2 ergibt sich

U_{R2 max} = U_{BE T2} = 2,25 V

Bei dieser – relativ hohen - Basisspannung sollte T2 ebenfalls voll durchschalten.

Belasteter Spannungsteiler – neue Näherungen für I_{B T1}und U_{BE T2}

Mit dieser Näherungsberechnung bleibt jedoch der belastete Spannungsteiler, gebildet aus T1, R2 und T2 unberücksichtigt. Je mehr Strom über die Basis-Emitter-Strecke von T2 fließt, desto weniger Spannung fällt an R2 ab. Bei U_{R2 max} = 2,25 V und U_BE
T2 = 0,7 V ist zu erwarten, dass der größere Teil von I_{C T1} über die Basis-Emitter-Strecke von T2 abfließen wird. Damit verringert sich der Spannungsabfall an R2 was wiederum I_{B T2} senkt.

Bei einem - aufgrund dieser Überlegung - neu geschätzten U_{R2 neu} = 1 V ergibt sich als neue Näherung
für I_{B T1}:

I = U / R

I_{B T1 neu}= (9,0 V – 0,7 V – 1,0 V) / 28 kOhm

I_{B T1 neu} = 7,3 V / 28 kOhm

I_{B T1 neu} ~ 261 uA

I_{B T1 neu} ist demnach also um 45 uA höher als das vorherige I_{B T1}. Das macht bez. Durchschalten des Transistors keinen Unterschied, s. Kennlinienfeld. Bei beiden Basisströmen schaltet T1 voll durch.

Für U_BE
T2 ergibt sich neu:

U_{R2 max neu} = U_{BE T2 neu} = 1,0 V

Auch bei dieser Basis-Emitterspannung ist davon auszugehen, dass T2 voll durchschaltet.

Berechnung maximaler Kollektorstrom T2

Bei voller Durchschaltung fallen an der Kollektor-Emitter-Strecke von T2 geschätzt ca. 0,1 Volt ab. Der Spannungabfall an LED2 (rot) wird mit 1,6 V angenommen.

R_V = (U_E – U_F) / I_LED

2,2 kOhm = (9,0 V - 1,6 V – 0,1 V) / I_{C
T2 max}

I_{C T2 max} = 7,3 V / 2,2 kOhm

I_{C T2 max} ~ 3,32 mA

Simulation mit EveryCircuit

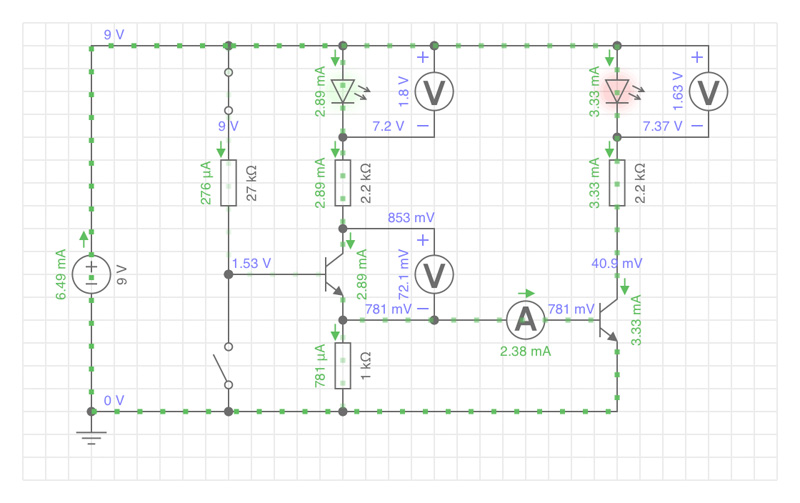
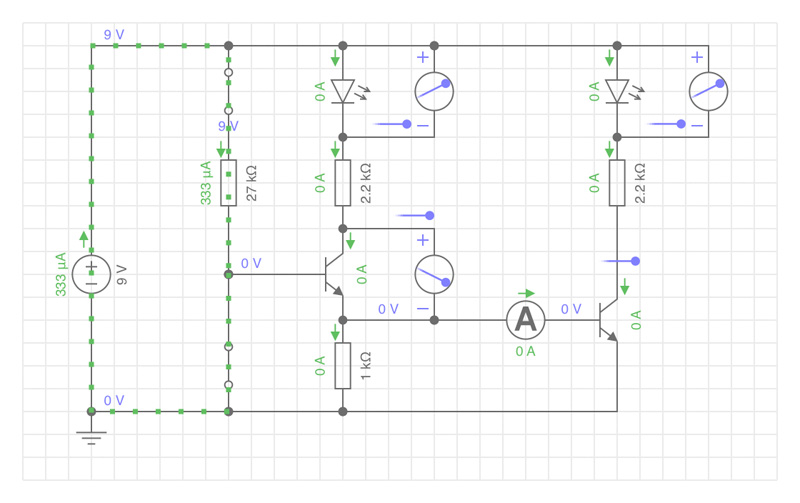
2 x Transistor BC547C

Für die Simulation angenommen: B = 500

Schalter 1 = geschlossen

Schalter 2 = offen

2 x Transistor BC547C

Für die Simulation angenommen: B = 500

Schalter 1 = geschlossen

Schalter 2 = geschlossen

Durch das Kurzschließen der Basis-Emitter-Strecke T1 schalten beide Transistoren nicht durch, keine der beiden LEDs leuchtet. Die Eingangsspannung fällt vollständig an R1 ab.

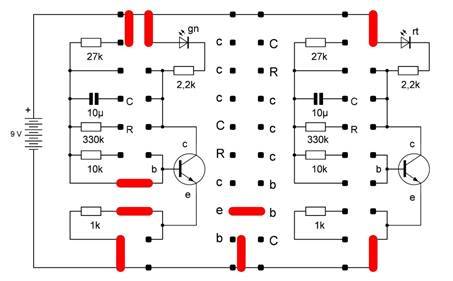
Aufbau der Schaltung am Steckbrett

Schalter 1 = geschlossen

Schalter 2 = offen

Schalter 1 = geschlossen

Schalter 2 = geschlossen

Schaltungswerte

Spannungen

	Berechnung/ Schätzung (V)	Simulation (V)	Messung (V)
U_{CE T1}	0,10	0,07	0,03
U_{CE T2}	0,10	0,04	0,01
U_{BE T1}	0,70	0,75	0,69
U_{BE T2}	1,00	0,78	0,76
U_LED1	1,70	1,80	1,94
U_LED2	1,60	1,63	1,88
U_R2	1,00	0,78	0,76
U_R3	-	6,35	6,18
U_R4	-	7,33	7,02

Ströme

	Berechnung (mA)	Simulation (mA)	Messung (mA)
I_{C T1 max}	2,25	2,89	2,81^*
I_{C T2 max}	3,32	3,33	3,19⁺
I_{B T1}	0,26	0,28	-
I_{B T2}	-	2,38	2,32

Messung Basisstrom Transistor T2

Fazit

Für die Handberechnung/Schätzung der Werte dieser Schaltung war schon einiger Denk- und Rechenaufwand nötig. Die Ergebnisse von Berechnung/Schätzung, Simulation und Messung stimmen insgesamt gut überein. Allerdings bestanden Unsicherheiten bei der Schätzung der Auswirkung des belasteten Spannungsteilers. Da ich es leider verabsäumt hatte, den Spannungsabfall an R1 zu messen, konnte ich den Basisstrom für T1 auf Basis dieser Messung nicht errechnen (I = U/R).

Dennoch stellt sich die Frage, ob man angesichts des Aufwands die Handberechnung bzw. Schätzung nicht auslassen kann und besser gleich den Schaltungssimulator startet.

Das würde für eine bereits fertig dimensionierte Schaltung wie die vorliegende sicher mehr Sinn machen. Steht man aber vor der Aufgabe, eine Schaltung neu zu entwickeln und ihre Bauteile zu dimensionieren, braucht man für den Schaltungssimulator sinnvolle Startwerte. Ansonsten müsste man jedes simulierte Bauteil auf gut Glück einstellen und die Schaltung dann über Änderungen der Werte hintrimmen. Das kann nicht Sinn der Sache sein, und so lohnt es sich, eine Handberechnung -oder zumindest eine Schätzung der Werte - für jede Schaltung durchzuführen, die man aufbauen möchte oder für die man sich interessiert. Das kommt auch der eigenen Erfahrung zugute und man entwickelt ein Gefühl dafür, ob man noch „im grünen oder bereits weniger grünen Bereich“ der Realität liegt. Was natürlich erst durch eine endgültige Messung der Schaltung am Steckbrett festgestellt werden kann.

Schaltungssimulation – Literaturempfehlung

Ich bin bei dieser Gelegenheit auch der Frage nachgegangen, wie Schaltungssimulatoren arbeiten. Kurz gesagt: unter der Anwendung der Gesetze von Kirchhoff, Ohm und numerischer Verfahren zur Berechnung nichtlinearer Schaltungen (für die das Ohm’sche Gesetz nicht gilt). Das ist das Gebiet der fortgeschrittenen Mathematik mit Gleichungen, Funktionen und Ableitungen, das im Verbund mit der hohen Rechenleistung aktueller Computer (PC, Mac, Smartphones) die Simulation auch komplexer Schaltungen in nahezu Echtzeit ermöglicht. Damit wird die Analyse auch umfangreicher Schaltungen möglich.

Eine sehr gute Übersicht und Einführung zu diesem Thema – auch für interessierte Laien verständlich - bietet das Buch „Analyse linearer und nichtlinearer elektrischer Schaltungen: Ein Kompendium“ von Prof. Andreas Gräßer.

Der Autor beschreibt, nach einer Einführung in die Grundlagen der Schaltungsanalyse, die Unterschiede zwischen linearen und nichtlinearen Schaltungen und erläutert die verschiedenen Methoden zur Berechnung für Gleich- und Wechselspannungen. Gezeigt wird unter anderem, wie mit der Schnittpunktmethode - auch ohne Schaltungssimulator – die Werte einer einfachen nichtlinearen Schaltung (zB LED mit Vorwiderständen) grafisch ermittelt werden können. Ein „Crash course“ stellt PSpice, einen der bekanntesten Schaltungssimulatoren, anhand praktischer Beispiele vor.

Das Buch ist sehr übersichtlich gestaltet und eignet sich, auch aufgrund seiner klaren Sprache und bildhaften Veranschaulichung komplizierter Sachverhalte, hervorragend für das Selbststudium. Auch wenn man nicht (mehr) über fortgeschrittene Mathematikkenntnisse verfügt, erhält man damit zumindest einen Eindruck, wie Schaltungssimulatoren arbeiten und was alles an Rechenarbeit „dahintersteckt“. Das hilft nicht zuletzt beim Einordnen und Bewerten der Ergebnisse einer Schaltungssimulation.

Empfehlung!

^_____

^* IC T1 max = UR3 / R3 = 6,18 V / 2,2 kOhm ~ 2,81 mA

⁺ IC T2 max = UR4 / R4 = 7,02 V / 2,2 kOhm ~ 3,19 mA

(Kommentar B.K: In der Praxis wird oft mehr geschätzt als gerechnet. Die Überschlagsrechnung zeigt, dass beide Transistoren ganz oder gar nicht schalten: Verhältnis der Widerstände an T1 ist 27 k zu ca. 2,2 k, ca. Faktor 10, also viel kleiner als die Strombestärkung, damit schaltet der Transistor voll durch. Die Basis von T2 begrenzt die Emitterspannung von T1 auf 0,7 V, durch den Emitterwiderstand fließt der kleinere Strom, 0,7 mA. T2 ist auf jeden Fall voll durchgeschaltet, weil fast der volle Kollektorstrom von T1 durch die Basis fließt. Das bedeutet, dass eine genauere Rechnung nicht mehr nötig ist. Änderungen der Widerstände zwischen -80% und +100% würden sich kaum auswirken.

Dass die CE-Restspannung bei T2 kleiner ist als bei T1, hätte ich auch geschätzt. Aber die genau gemessenen Werte sind sehr interessant. Und interessant ist auch, dass die Simulation in dem Punkt relativ stark daneben liegt. Dafür gibt es nämlich keine richtige Formel, und jeder Transistor ist etwas anders.)

Elektronik-Labor Projekte Lernpakete Grundschaltungen