4.1 Laden und entladen
In diesem Versuch aus der Reihe „Grundschaltungen
der Elektronik“ von Burkhardt Kainka wird gezeigt, dass ein Kondensator
Ladung aufnehmen und abgeben kann. Mit der aufgenommenen Ladung soll der
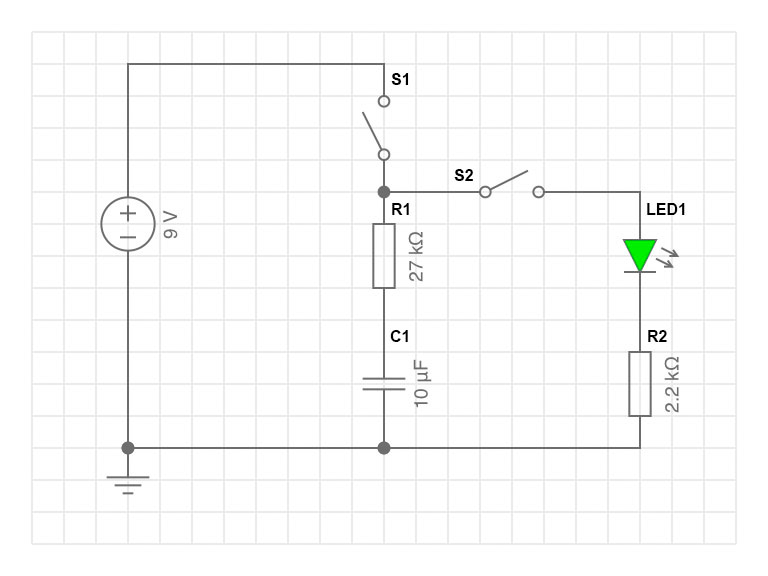
Kondensator eine grüne LED zum Aufleuchten bringen. Dazu wird für den Versuchsaufbau auf dem
Steckbrett ein metallisierter Polyester-Kondensator (10 uF, Folie, ungepolt)
verwendet. Auf der Platine im Lernpaket sind keramische Vielschicht-Kondensatoren. Der Kondensator wird über einen
27-Kiloohm-Widerstand geladen. Das bedeutet, dass die Aufladung nicht im
Augenblick – als Kurzschluss -, sondern zeitverzögert erfolgt. Die Entladung geschieht über eine
Reihenschaltung aus LED und 2,2-Kiloohm-Widerstand. Über Schalter S1 wird der Kondensator
geladen, über S2 entladen.
Berechnung Ladung und Entladung
Die Ladezeit eines Kondensators hängt von
seiner Kapazität sowie von seinem vorgeschalteten Widerstand ab. Die Zeitkonstante Tau in Sekunden gibt an,
wie schnell die Spannung am Kondensator ansteigt. Nach Tau = 5 (jeweils fünf gleiche
Zeitintervalle) ist ein Kondensator zu nahezu 100 Prozent aufgeladen, bei Tau =
1 zu 63 Prozent. Das bedeutet, dass der Kondensator zu Beginn rasch lädt und
dann zunehmend langsamer. Umgekehrt gilt dasselbe für die Entladung –
schnelle Spannungsverminderung zu Beginn, dann immer langsamer. Ladung und Entladung folgen
Exponentialfunktionen, die zugehörige Spannungs-/Zeit-Kurven verlaufen daher nicht
linear, das erklärt das beschriebene Lade- und Entladeverhalten.
Berechnung
der Ladekurve
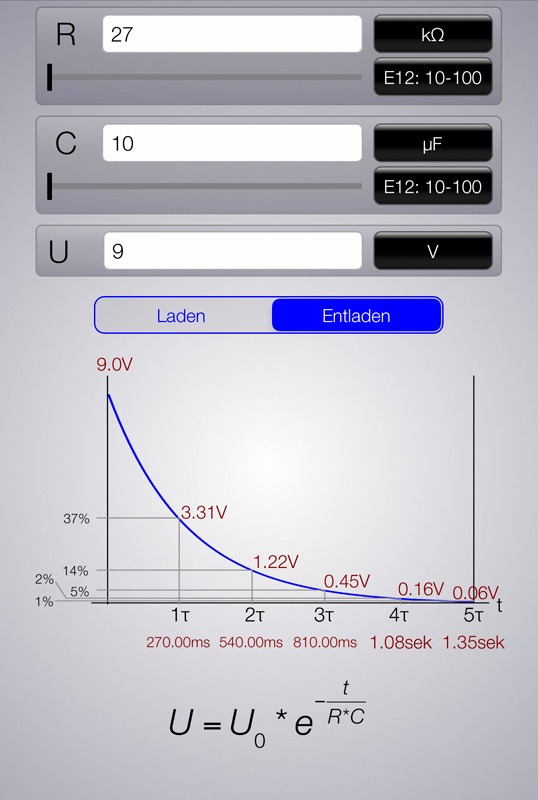
Das folgende Bild zeigt die Eingabemaske
zur Berechnung der Ladekurve eines Kondensators in Electronics Engineering ToolKIT PRO, eine
App für Elektronik (iOS).
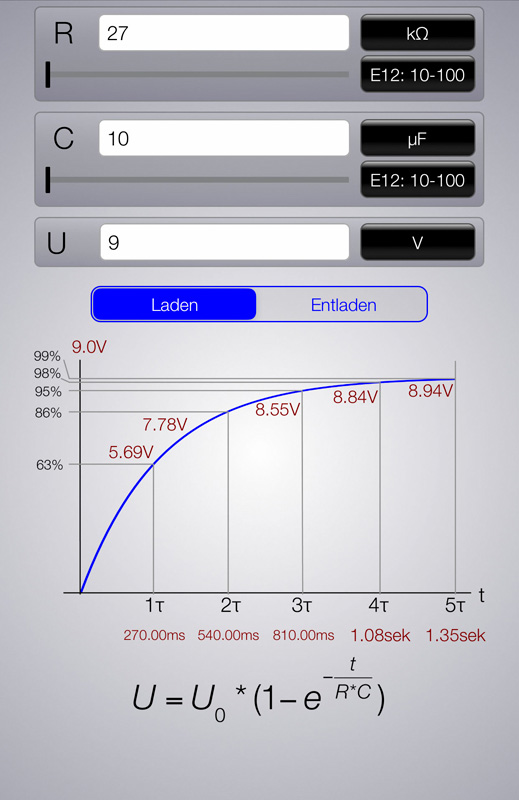
Eingegeben werden die Werte für Vorwiderstand (Volt), Kapazität (Farad) und Ladespannung (Volt). Daraus errechnet die App fünf Wertepaare Kondensatorspannung in Volt/Tau in Sekunden und zeigt damit an, nach welchem Zeitintervall welche Aufladung erreicht ist. Unter dem Diagramm wird die für die Berechnung zugrundeliegende Formel für die Ladung eines Kondensators angezeigt:
U = Kondensatorspannung (Volt)
U0 = Ladespannung (Volt)
e = Eulersche
Zahl
t = Zeit (Sekunden)
R = Widerstand (Ohm)
C = Kapazität des Kondensators (Farad)
Aus der Formel wird ersichtlich, dass eine
Handberechnung zeitaufwändig/umständlich ist und daher – ohne schlechtes
Gewissen ;-) an die Software delegiert wird.
Entladekurve
Dieses Bild zeigt die Entladekurve, die genau entgegengesetzt zur Ladekurve verläuft. Die Tau-Zeitintervalle bleiben gleich, beziehen sich jetzt aber auf die abnehmende Kondensatorspannung.
Allerdings kann die Entladekurve der
vorliegenden Schaltung nicht mit
diesem Tool berechnet werden, da die Reihenschaltung für die Entladung aus einem
linearen Widerstand und einer nichtlinearen LED besteht.
Ein Wert für einen Ersatzwiderstand zur
Eingabe in das Tool kann aus diesen beiden Bauteilen (nach dem Ohm’schen Gesetz)
nicht gebildet werden. Daher wird das Entladeverhalten im Schaltungssimulator EveryCircuit untersucht.
Ladung
Q
Die Ladung Q eines Kondensators in Coulomb kann nach der Formel
Q = C
* U
berechnet werden.
C = Kapazität des Kondensators in Farad
U = Ladespannung in Volt
Für die vorliegende Schaltung ergibt sich:
C = 10 uF
U = 9 V
Q = (10*10-6 F)*(9*100 V)
Q = 90*10-6 C = 90 uC (90
Mikrocoulomb, das entspricht einem Strom von 90 uA, der eine Sekunde lang fließt)
Dieser Strom von 90 uA fließt allerdings
nicht eine Sekunde lang gleichmäßig durch die LED, sondern exponentiell
abnehmend, wobei die Entladung des Kondensators zu Beginn am größten ist. Daher
ist weniger mit einem Leuchten als mit einem Aufblitzen der LED zu rechnen.
Schaltungssimulation in EveryCircuit
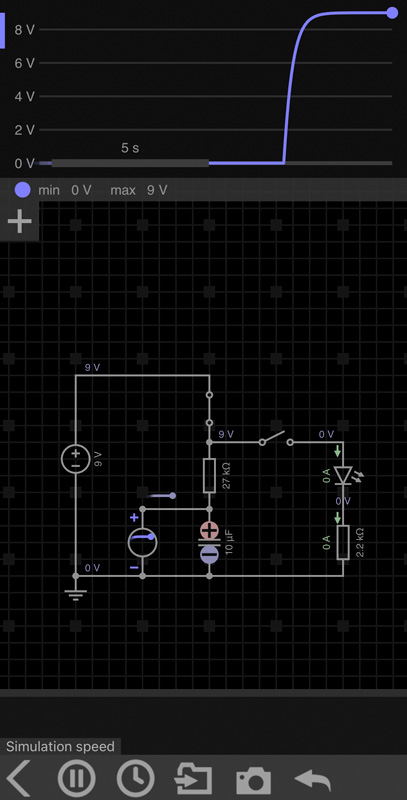
Das folgende Bild zeigt die Ladekurve des
Kondensators.
S1
ist geschlossen, S2 geöffnet. Die
Kondensatorspannung steigt exponentiell bis zur Ladespannung an. Nach
vollständiger Ladung leitet der Kondensator Gleichstrom nicht mehr und sperrt.
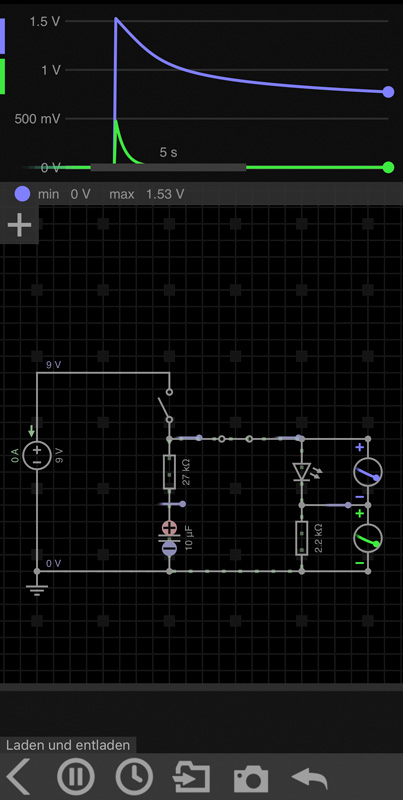
Nun wird S1 geöffnet und S2 geschlossen. Der Kondensator entlädt über die LED und den Vorwiderstand, wobei die Spannung – und damit der Strom – zu Beginn rasch kleiner wird. Die violette Kurve zeigt den Verlauf des Spannungsabfalls an der LED, die grüne Kurve den Verlauf am Vorwiderstand. Die LED leuchtet in der Simulation schwach auf. Hier wird deutlich, dass die Kennlinie einer LED ebenfalls exponentiell verläuft. Der Verlauf des Spannungsabfalls nach Absinken unter den Schwellspannungs-Punkt erfolgt zunehmend flacher, da sich der Diodenwiderstand erhöht. Ein immer kleinerer Strom fließt somit aus dem Kondensator durch die LED, deren Widerstand zunehmend größer wird, beide Phänomene „halten die Kurve flach“. Der Spannungsabfall am Vorwiderstand entspricht hingegen der Entladekurve des Kondensators, die auch in der App (siehe Bild oben) zu sehen ist. Die Spannung fällt exponentiell - und schneller als an der LED - auf 0 Volt.
Aufbau der Schaltung am Steckbrett
Zum Einsatz kommt wieder das Experimentier-Steckboard
EXSB1 von ELV das oft benötigte Bauteile
und Anschlüsse außerhalb des Steckbretts bereithält und damit Platz spart. S1 und S2 werden über die Schalter S3 und S4 unterhalb des Steckbretts realisiert. Nach Aufladen des Kondensators über S1 und
Öffnen von S2 leuchtet die grüne LED kurz auf (leider nicht im Foto sichtbar).


Das
Experimentier-Steckboard EXSB1 in der Gesamtsicht
Links
oben der Bereich für den Spannungseingang, links darunter die Schaltung für
einen Rechteckgenerator. Am unteren Rand Massepunkte, Trimmer, Schiebeschalter,
Taster, rechts oben Cinch- und BNC-Buchse, LEDs zur freien Beschaltung,
Klemmbrücken sowie Messpunkte.
Messungen mit dem Oszilloskop
Die Anzeige von Spannungsverläufen über
Zeit ist die Domäne des Oszilloskops. Während das klassische Multimeter
Augenblickswerte angibt, werden mit dem Oszilloskop Veränderungen im
Spannungsverlauf sichtbar. Zum Einsatz kommt das kleine Digital-Oszilloskop
DSO138,
das mit einem Kaufpreis von unter 50 Euro zu den preisgünstigsten
Modellen zählt. Nichtsdestotrotz bietet es alle für die anstehende
Aufgabe
benötigten Funktionen und es macht zudem Spaß, mit dem Gerät zu
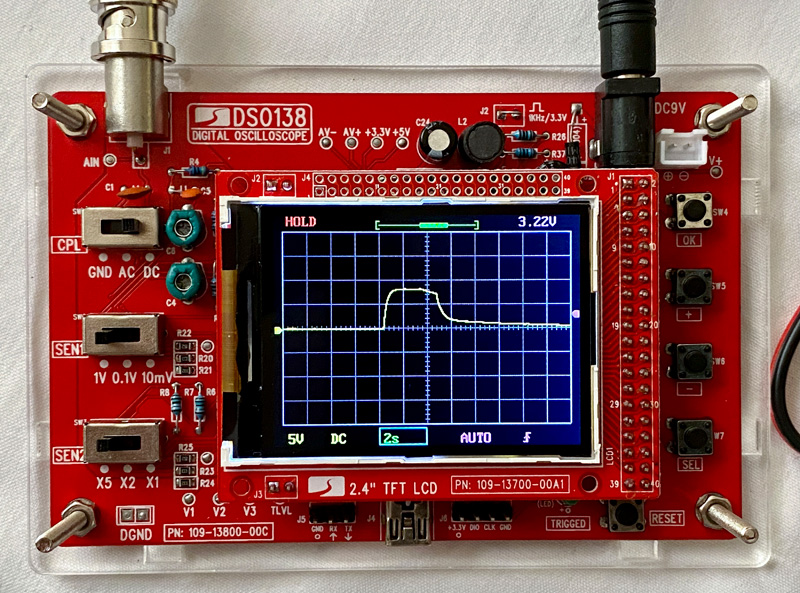
arbeiten. Das erste Bild zeigt den exponentiellen Spannungsverlauf
bei Ladung und Entladung des Kondensators. Auf der Y-Achse (vertikal)
wird die
Spannung angezeigt, auf der X-Achse (horizontal) die Zeit in Sekunden.
Das
Oszilloskop ist so eingestellt, dass ein Kästchen des Gitters 5 Volt/2
Sekunden
entspricht. Da der Polyester-Kondensator in Blockform direkt auf dem
Steckbrett
aufliegt, ist ein Spannungsabgriff mit Klemmfedern nicht möglich. Es
wird daher
die Spannung am Ausgang von R1 und an Masse abgenommen, dazwischen
liegt C1, an
dem die Spannung abfällt. Nach Schließen von S1 (S2 offen) lädt der
Kondensator auf bis die Ladespannung von 9 Volt erreicht ist. Es fließt
kein
weiterer Strom mehr durch den Kondensator, die anliegende Ladespannung
bleibt
konstant bis S1 geöffnet wird. Nun fällt die Kurve leicht ab, da der
Kondensator über das Oszilloskop mit seinem Innenwiderstand von 1
Megaohm
entlädt. S2 wird geschlossen, die Entladung erfolgt exponentiell über
die LED
und den Vorwiderstand bis nahe 0 Volt.
Die Spannungsverminderung an R2 zeigt den abnehmenden LED-Strom während der Entladung (Anzeige: 0,2 Volt/0,2
Sekunden).
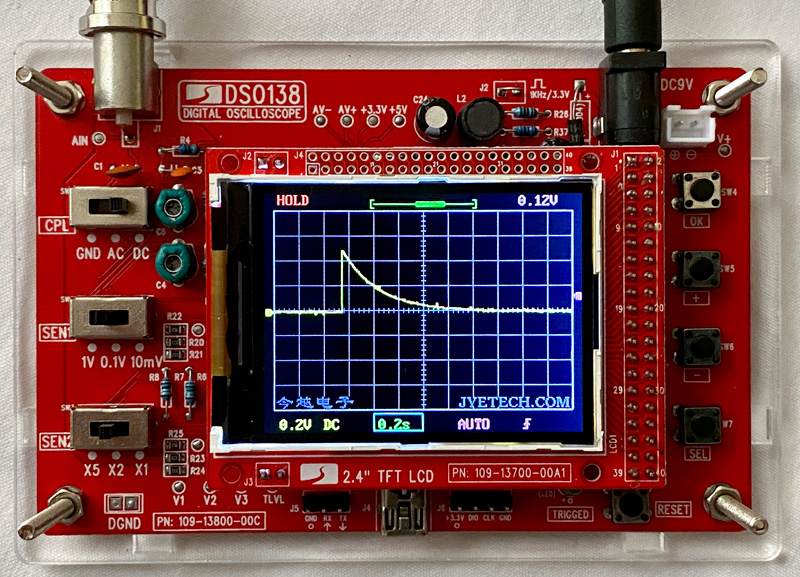
Grund dafür ist der nichtlineare
Spannungsverlauf an der LED. Nach Unterschreitung ihres Schwellenpunktes sperrt
die LED zunehmend, wodurch der Spannungsabfall an ihr nur langsam kleiner wird.
Da die LED in Reihe mit dem Widerstand liegt und einen zunehmend größeren
Widerstand aufweist, fällt die Restspannung mehr und mehr an ihr ab. Dadurch
geht die Spannung an R2 - früher als bei der LED - auf Null.

Abnahme
der Spannung an R2 mit zwei Federklemmen.
Die
orangefarbene LED rechts gehört nicht zur Schaltung und zeigt an, dass Spannung
am Bus des Steckbretts anliegt (freie Beschaltung).
Fazit
Auch diesmal stimmen Schaltungssimulation
und Messung am Steckbrett gut miteinander überein. Es konnte gezeigt werden,
dass die Ladung und Entladung des Kondensators nicht gleichförmig, sondern entlang
exponentiell verlaufenden Kurven erfolgt. Der größte Strom fließt zu Beginn der
Entladung, die LED blitzt auf. Das kleine Digital-Oszilloskop
DSO138 hat sich bewährt und kommt insbesondere einem schmalen
Hobby-Budget entgegen. Da es nur über grundlegende Funktionen verfügt, ist es
ein ideales Einstiegsgerät, das zu Beginn nicht mit Funktionsvielfalt überfordert. Mit dem Kondensator als Bauteil können in
einer Gleichspannungs-Schaltung periodische Spannungsänderungen erzeugt werden.
Damit lassen sich, zusammen mit anderen Bauteilen, zeitabhängige Schaltungen
realisieren, wie zB Dimmer-Schaltungen oder Kippstufen. Aber auch für kreative Bastler bieten sich
interessante Möglichkeiten, wie die weiteren
Kondensator-Schaltungen von Burkhardt Kainka zeigen, die hier noch
besprochen werden.