Der Philbrick Phasenschieber und Oszillator
Peter Gerber, HB9BNI
Ausgelöst hat diese Betrachtung Burkhard Kainka, DK7JD mit seinem Orgelbausatz bzw seinem Sinusoszillator mit einem Transistor[, der als Emitterfolger arbeitet und damit eine Spannungsverstärkung von kleiner als 1 hat. Der Oszillator sollte also nicht funktionieren, tut dies aber doch, weil das Rückkoppelungsnetzwerk die Spannung verstärkt bzw „überhöht“. Beim Lesen des Beitrags von OM Norbert Renz, OE9NRH[, habe ich mich an das Philbrick-Netzwerk und an den damit konstruierbaren Oszillator erinnert. Dieser Oszillator funktioniert nach dem gleichen Prinzip: der Verstärker hat eine Spannungsverstärkung von 1 oder <1, das Netzwerk verstärkt bzw „überhöht" die Spannung.
Eigentlich braucht der Verstärker eines Oszillators „nur" eine Leistungsverstärkung. Sollte die Ausgangsspannung des Verstärkers kleiner als die benötigte Eingangsspannung sein, kann man ja immer einen Transformator zwischenschalten und so die Amplitude erhöhen. Nach der ersten erfolgreichen Demonstration des Transistors als Verstärker (am 23. Dezember 1947, laut der Originalseite des Laborbuches steht zwar 24. 12. 1947, der Eintrag dürfte am Folgetag gemacht worden sein, ich hätte auch erst mal gefeiert) soll der Laborleiter Ralph Bown, damals Vizepräsident der Entwicklungsabteilung der Bell Laboratories, gefordert haben, dass damit ein Oszillator gebaut werden könne (Jon Gertner : The Idea Factory, p 97)].

Da das Signal an einem der (genau gleich konstruierten) Spitzenkontakte eingespeist und am anderen Spitzenkontakt ausgeleitet wurde (heute würde man von Emitter bzw Kollektor sprechen), hatte der Verstärker an sich keine Spannungsverstärkung, aber zwei Transformatoren, nicht zuletzt für die Impedanzanpassung; das Ding muss äusserst hochohmig gewesen sein.
 Philbricks Patent
Philbricks Patent
Es geht dabei um das Patent US 2’730'679. Eine Analyse des Patenttextes zeigt: Der Zweck der patentierten Schaltung ist es nicht, in einem Oszillator eine Spannungsüberhöhung zu erzeugen, zumindest nicht dauerhaft und nicht bei einer Sinusschwingung. Philbrick erklärt den Zweck wie folgt (die Bilder stammen aus der Patentschrift)
Wenn die Spannung einer Sprungfunktion (Heaviside-step. Oliver Heaviside wäre eine eigene Betrachtung zu gönnen. Er hat die Sprungfunktion die Anfangs des 20. Jahrhunderst meist seinen Namen trug zwar nicht erfunden, aber sehr bekannt gemacht. Es gibt nicht viel Literatur über Heaviside, aber immerhin zwei gute Biografien mit reichlich wissenschaftlichem Beiwerk: Nahin: Oliver Heaviside. The Life, Work, and Times of an Electrical Genius of the Victorian Age. Und: Mahon: The Forgotten Genius of Oliver Heaviside. A Maverick of Electrical Science. Heue ginge Heaviside problemlos als “Schwerer Asperger” durch.) wie diese

an einen gewöhnlichen RC Hochpass gelegt wird (z.B. an den Eingang eines Oszilloskopes mit AC-Koppelung, diese Dimensionierung ist in meinem KO von 1970 realisiert),
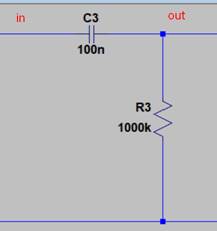
so resultiert am Ausgang des Hochpasses und damit auf dem Bild des KO’s ein Verlauf wie dieser

Die Ausgangsspannung steigt rasch an (abhängig vom Innenwiderstand der Spannungsquelle), dann fällt die Ausgangsspannung exponentiell ab.Die Zeit, die das Signal braucht bis es nahezu wieder 0 ist (die Formulierung des Patentanwaltes, Elektroniker würden wohl sagen "auf 1/e abgefallen ist), hängt von der Grenzfrequenz (also von der Zeitkonstante) des RC-Hochpasses ab.
Ist die Stufenspannung am Anfang von einer hochfrequenten Schwingung überlagert
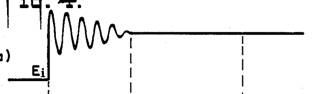
so wird durch diesen exponentiellen Abfall das Signal nach dem RC-Hochpass verzerrt. Der Mittelwert der schnellen Oszillation wird nicht konstant dargestellt, sondern abfallend.

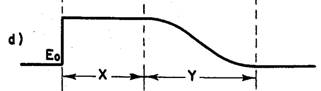
Das von Philbrick patentierte Netzwerk reagiert anders. Bei einer reinen Sprungfunktion wird nach Durchlauf durch das patentierte Netzwerk am Ausgang dieser Spannungsverlauf entstehen
Ist die Stufenspannung am Anfang von einer hochfrequenten Schwingung überlagert, dann entsteht dieser Verlauf der Ausgangsspannung
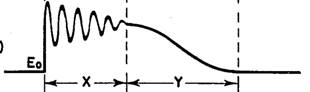
Der Anfang der Stufenfunktion + hochfrequenter Schwingung wird praktisch unverzerrt übertragen, erst nach einer wählbaren (durch die Dimensionierung der R's und C’s) Zeit fällt die Ausgangsspannung wieder mehr oder weniger exponentiell auf 0 zurück. Im Lichte der folgenden Diskussion könnte an sagen: Für tiefe Frequenzen findet eine Spannungsüberhöhung statt, die bei hohen Frequenzen fehlt.
Philbrick nennt seine Erfindung ein „delayed-recovery high-pass filter network". Es kann mit 2, 3, ..., n Stufen ausgeführt werden.
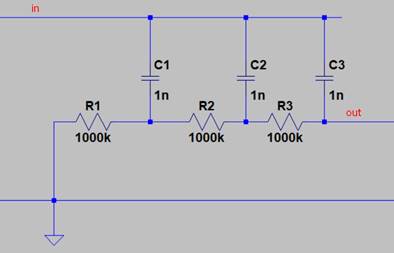
Hier ein dreistufiges Netzwerk, wie im Patentantrag beschrieben. Man beachte die relativ kleinen Kondensatoren und die hohen Widerstände (1 MOhm¨)
Philbrick gibt weiter an, dass die Länge der Zeit mit annähernd konstanter Übertragung (in zwei der obigen Abbildungen als X bezeichnet) grösser wird und die Länge des Abfalls des Signals (oben mit Y bezeichnet) kleiner wird, wenn die C's vom Eingang zum Ausgang des Netzwerkes grösser und die R’s in gleicher Richtung kleiner werden. Dabei sollten die Zeitkonstanten (also das Produkt R*C) jeder Stufe annähernd konstant bleiben.
Zur Dimensionierung eines 3-stufigen Netzwerkes schreibt Philbrick:

ein dreistufiges Filter mit C 1,2,3 von 10nF, 20nF, 50nF und R 1,2,3 von 3.3MOhm, 1MOhm, 0.5Mohm soll eine 10 Millisekunden lange unveränderte Passage (X) des Signals und eine Rückkehrzeit (Y) von 100 Millisekunden ergeben. Dies bei einer Quellenimpedanz von 1kOhm und einer Lastimpedanz von 100 MOhm.
Das Patent wurde 1951 eingereicht und 1956 erteilt.
Grund und Zweck der Erfindung
In der Patentschrift wird nicht erwähnt, wieso Philbrick die Darstellung eines Spannungssprungs mit überlagerter hochfrequenter Oszillation am Oszillograf verbessern wollte. Solche Phänomene treten ja eher selten auf und wenn, dann meist als unerhebliche Begleiterscheinungen.
Ein Grund könnte eine frühere Erfindung von Philbrick gewesen sein, der „Polyphemus“. Das war ein einfacher Analogrechner, bestehend aus einem mehrstufigen Verstärker, einem RC-Netzwerk mit variablen R’s und C’s, dessen Konfiguration mit Steckern und Kabel verändert werden konnte und einem Oszillografen zur Darstellung des Resultats. Ein Bild[5] aus seinem Laborbuch von ca 1938 (Per A. Holst: George A. Philbrick and Polyphemus-The First Electronic Training Simulator. Annals of the History of Computing, Volume 4, Number 2, April 1982 • 143ff) zeigt das Prinzip
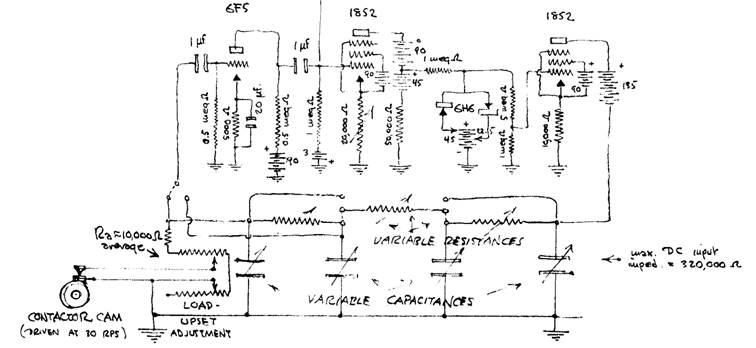
Oben ein (in diesem Fall dreistufiger) RC-gekoppelter Röhrenverstärker, der auch einen Begrenzer mit zwei antiparallel geschalteten Dioden enthält, unten das variable und veränderbare RC-Rückkoppelungsnetzwerk. Die Leitung nach oben nach der ersten Röhre (6F5) geht zum KO. Vielleicht sind bei Versuchen mit diesem Apparat solche Schwingungen aufgetreten, die Philbrick besser sehen/messen wollte.
Analogrechner waren ja sowieso das Hauptgeschäft von Philbrick. Er hat etwas später dann auch den Bau des ersten Operationsverstärkers angeregt (Julie und Ragazzini, Columbia University). Das steckbare Modul hatte 2 Röhren mit total 4 Trioden, einen Differenzverstärker „moderner“ Art mit einem + und einem – Eingang, eine Spannungsverstärkung von etwa 25'000 und ein Verstärkungs-Bandbreitenprodukt von 1 MHz. Von diesem Modul setzte er bis zu 40 Stück ein in seinem Analogrechner für die Berechnung von Geschossbahnen.
Das Philbrick-Netzwerk als Phasenschieber
Dass man Philbricks Netzwerk auch als Phasenschieber benutzen konnte und dass man zusammen mit einem Verstärker auch einen Oszillator bauen konnte, daran dachte zunächst offenbar niemand.
Auf den „Philbrick-Oszillator“ bin ich im Buch „307 Schaltungen“ p249f gestossen. Man bezieht sich dort auf „electronic design, März 1996".
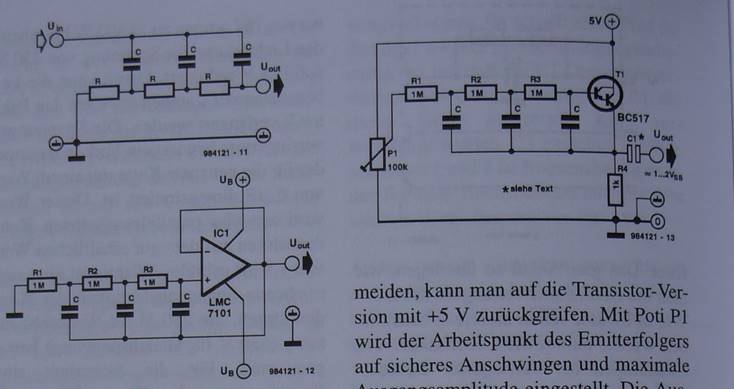
(so habe ich 2008 noch „digitalisiert“: Foto im Freien und im Schatten aufgenommen, wie man an der blauen Färbung des an sich weissen Papiers erkennt)
Mit einem R von 1 MOhm (hier ist ein Druckfehler im Buch, da steht MW! Der Setzer war wohl durch das W überfordert.) und C’s von 100nF soll man eine Frequenz von ca 5 Hz bekommen, mit 1 nF eine von 500 Hz. Die Transistorversion ist ebenfalls, wie der Transistor in Burkhard Kainkas Orgelbastelkasten ein Emitterfolger, dreht also die Phase nicht und die OpAmp-Version wird am + Eingang gespeist (hat also auch keine Phasendrehung) und hat eine Spannungsverstärkung von 1. Die Spannungsüberhöhung, von der Norbert Renz, OE9NRH berichtet, kommt also auch hier zum Tragen, sonst würde der Oszillator nicht schwingen.
Ein Nachbau in LTSpice scheiterte am fehlenden Power-Darlington, aber Operationsverstärker gibt es in LTSpice genug. Ich wählte den LT1797 (angepriesen als „rail -to- rail“:
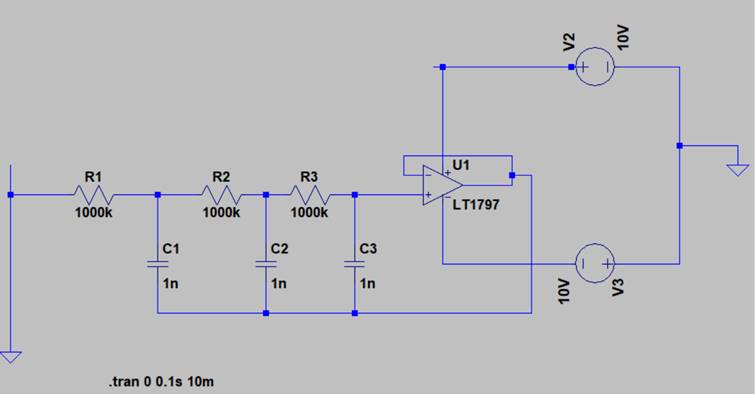
und, tatsächlich, schon nach 2 Perioden geht das Signal „rail -to- rail“. Der Oszi schwingt, aber das Signal ist kein Sinus, eher ein Rechteck. Die Spannungsverstärkung eines „Umgangs“ ist offenbar deutlich grösser als 1, obwohl der Verstärker eine Spannungsverstärkung von genau 1 hat.
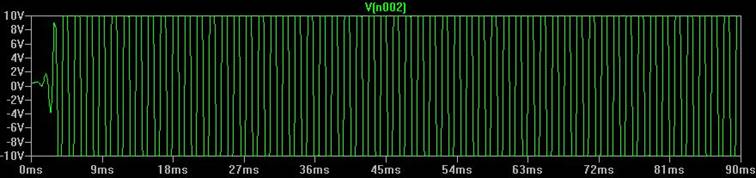
Um eine annähernd sinusförmiges Signal zu bekommen, habe ich einen Abschwächer (auf ca 90% der Ausgangsspannung) eingebaut sowie zusätzlich eine einfache Regelung mit 2 antiparallel geschalteten Siliziumdioden. (das ist natürlich nicht „state of the art“, auch nicht nach meinen eigenen Ansprüchen, quick and dirty eben)
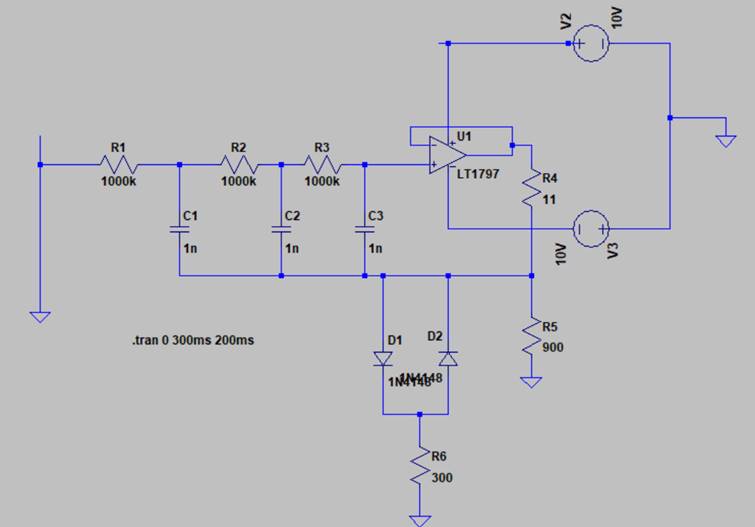
Das Signal sieht ansprechend aus (die deutlich längere Einschwingphase im Vergleich zum nicht geregelten Modell habe ich abgeschnitten). Die Frequenz mit 3 x 1 MOhm und 3 x 1 nF liegt bei 380 Hz.
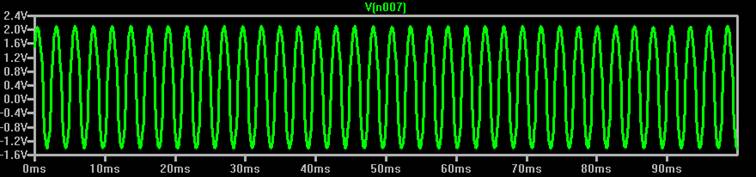
Das Spektrum sieht nicht berauschend aus, aber in Anbetracht der sehr rudimentären Regelung bin ich zufrieden. Alle Oberwellen sind um 20dB unter dem Signal.
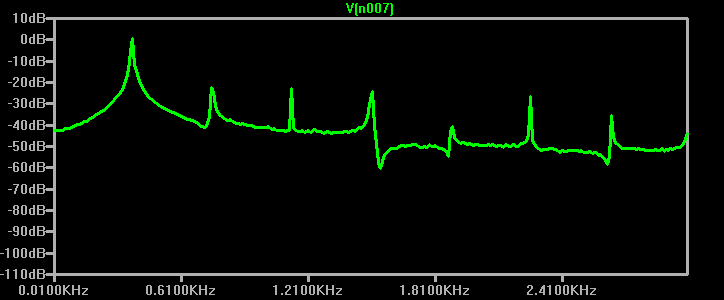
(Selbstverständlich sollte man bei, nun ja, „marginalen“ Daten dann natürlich eine lineare Darstellung wählen, sieht dann gleich sehr viel besser aus:
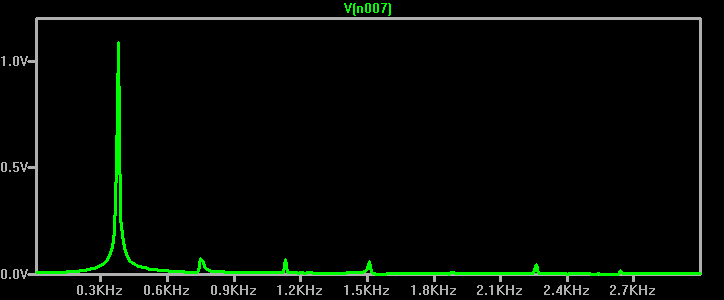 )
)
Experimente mit dem Philbrick-Netzwerk
Bode-Plot
Ich habe auch den Phasenschieber alleine gewobbelt. Eingangsspannung 5V, Dimensionierung wie oben: 3 x 1nF, 3 x 1MOhm.
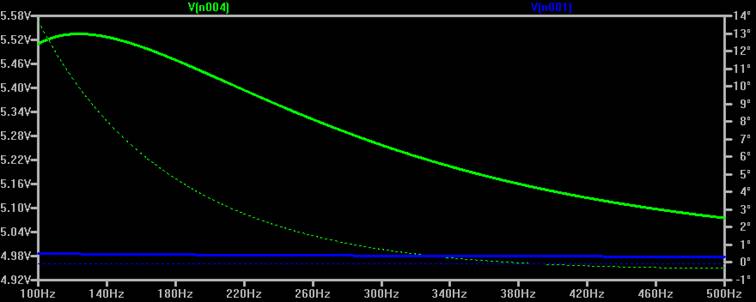
Blau = Eingang, 5.0 V. Die grün gepunktete Phase des Ausgangssignal schneidet die (Schlecht etwas unter der durchgezogenen blauen Amplitude sichtbare) blau gepunktete Linie (Phasenreferenz des Eingangs, rechte Skala bei 0 Grad) etwas oberhalb von 380 Hz. Man sieht gut auch die Spannungsüberhöhung, die bei ca 120 Hz maximal 0.54 V, also mehr als 10% der Eingangsspannung beträgt und bei der Schwingfrequenz noch 0.15 V = 3%.
Die obige Wobbelkurve lässt in meinem Gehirn allerdings auch deutlich „dunkelgelbe“ Warnlampen aufleuchten. Ab etwa 140Hz entspricht der Amplitudenverlauf einem Tiefpass: die Amplitude fällt mit zunehmender Frequenz. Bei einem einfachen RC-Tiefpass ist das verbunden mit einer negativen Phasenverschiebung. Hier ist die Phasenverschiebung aber positiv (maximal 13 Grad), nimmt aber, wie bei einem RC-Tiefpass weiter ab, um bei gut 380 Hz NULL zu erreichen. Irgendwo muss in diesem Netzwerk auch ein Hochpass vorhanden sein, der ja prinzipiell eine positive Phasenverschiebung hat. Das Vorhandensein sowol eines Hoch- wie Tiefpasses macht natürlich Sinn. Philbrick will sowohl die hochfrequente Oszillation wie auch die tieffrequenten Teile des horizontalen Verlaufs des Spannungssprungs übertragen. Den Hochpass (bzw die Hochpasse) sehe ich natürlich, die C’s in Serie mit einem R nach Masse. Aber wo ist in diesem Netzwerk der Tiefpass?
Sprungantwort und Spannungsüberhöhung
Die Antwort des Phasenschiebers auf einen Sprung der Eingangsspannung (also auf einen Heaviside step, das Thema des Patentes von Philbrick) sieht ebenfalls interessant aus: (Dimensionierung wie oben, 3 x 1 MOhm, 3 x 1 nF)
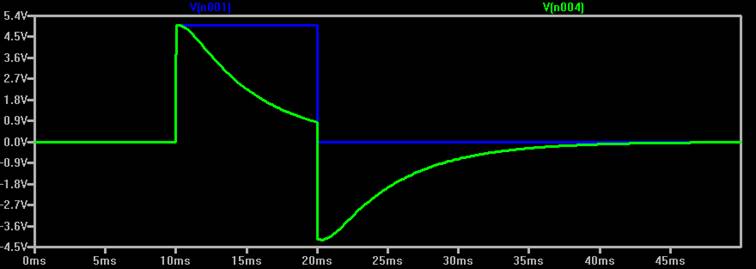
Blau: Eingangsspannung, ein 10 Millisekunden langer Spannungssprung von 0 auf 5 V. Grün das Ausgangssignal. Man sieht, dass das grüne Signal nicht direkt zu fallen beginnt, sondern eine kurze Zeit „oben“ bleibt. Das ist der Effekt, den Philbrick patentiert hatte.
Aber man sieht auch, wie die Spannungsüberhöhung bei einem relativ kurzen Rechtecksignal zustande kommt: nach dem Abschalten des Spannungssprungs fällt die Ausgangsspannung auf negative Werte, und das obwohl keine negative Gleichspannungsquelle vorhanden ist. Die Amplitude des grünen Ausgangssignals beträgt etwa 9Vss, obwohl das Eingangssignal nur 5 V ss hat.
Gross ist der Effekt bei der Dimensionierung 3 x 1 MOhm, 3 x 1 nF allerdings nicht. Ich habe auch das 3-stufinge Netzwerk aus dem Patentantrag mit der Dimensionierung 10nF, 20nF, 50nF und 3.3MOhm, 1MOhm, 500kOhm gemessen und erhalte (Einganssignal von 5 V weggelassen, da es das Ausgangssignal überdeckt, Pulsdauer jetzt 100 ms!)
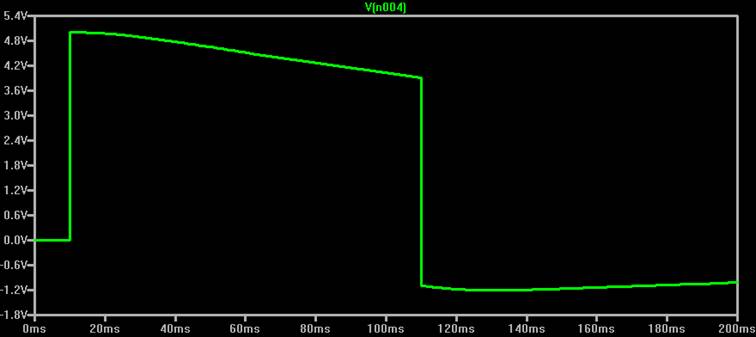
Verglichen mit einem einstufigen RC-Hochpass (20nF, 1MOhm, müsste eine 3dB Grenzfrequenz von 8 Hz ergeben) ist aber ein Unterschied in der Kurvenform schon zu sehen. Philbricks Eingangsnetzwerk für einen KO zeigt eine deutlich „natürlichere“ Nachbildung des relativ langen Rechteckimpulses als der übliche Hochpass.
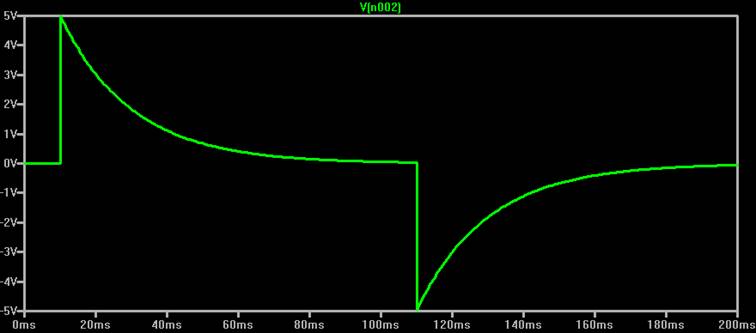
Intuitiv denke ich, dass bei einem mehrstufigen Netzwerk wie beim Philbrick-Netzwerk die Spannungsüberhöhung am besten funktioniert, wenn die Spannungsquelle einen möglichst geringen Innenwiderstand hat und am Eingang des Netzwerkes möglichst grosse Kondensatoren und möglichst kleine Widerstände liegen, damit möglichst rasch möglichst viel Energie ins Netzwerk gelangen. Am Ausgang sollten dann möglichst kleine Kondensatoren und möglichst grosse Widerstände liegen, was natürlich die Ausgangsimpedanz erhöht und einen hohen Eingangswiderstand des nachfolgenden Verstärkers erfordert, wenn man damit einen Oszillator bauen möchte.
Das kann man testen. Philbrick hat ja in seinem Patent empfohlen, für seine Zwecke (also für die möglichst naturgetreue Übertragung einer Sprungfunktion mit überlagerter höherfrequenter Schwingung) den Eingang des Netzwerkes mit hohen Widerständen und kleinen Kondensatoren auszustatten, den Ausgang umgekehrt, also gerade nicht wie die obige Intuition vermutet (die natürlich ein anderes Ziel hat, nämlich möglichst grosse Spannungsüberhöhung).
Grün ist die periodische Sprungantwort (100 ms on/100 ms off, blau) auf Philbrick’s Patentrezept
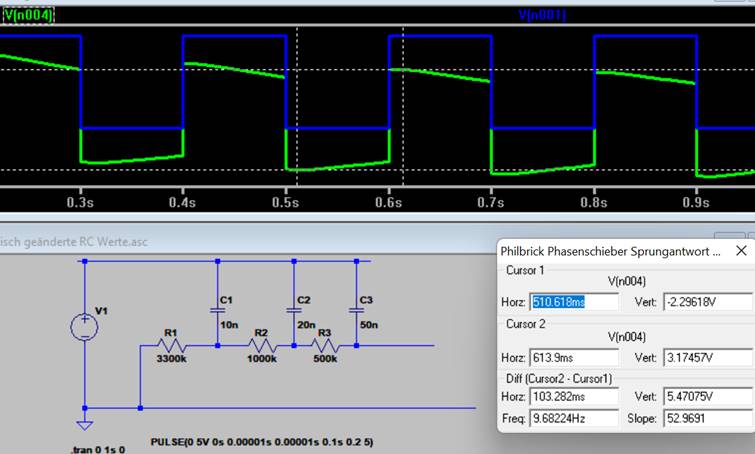
Spannung des Ausgangs 5.47Vss bei Eingang 5Vss. Der Ausgang hat natürlich nach genügend langem Vorlauf keinen Gleichspannungsanteil mehr. (die gepunkteten weissen Linien sind die beiden Cursor, die an der gürnen Ausgangskurve die beiden Messtellen markieren)
Wenn ich die Reihenfolge der 3 Stufen umkehre, also zuerst kleine Widerstände und grosse Kondensatoren verwende (meine Intuition für grosse Spannungsüberhöhung), sieht die Sache so aus
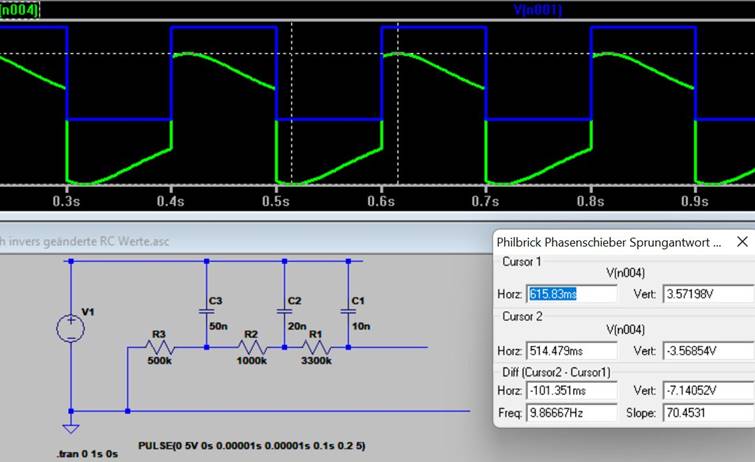
Spannung des Ausgangs 7.14 Vss bei Eingang 5Vss. Die Spannungsüberhöhung ist also tatsächlich grösser, wenn am Eingang grosse Kondensatoren und kleine Widerstände liegen!
CC BY-NC-ND