

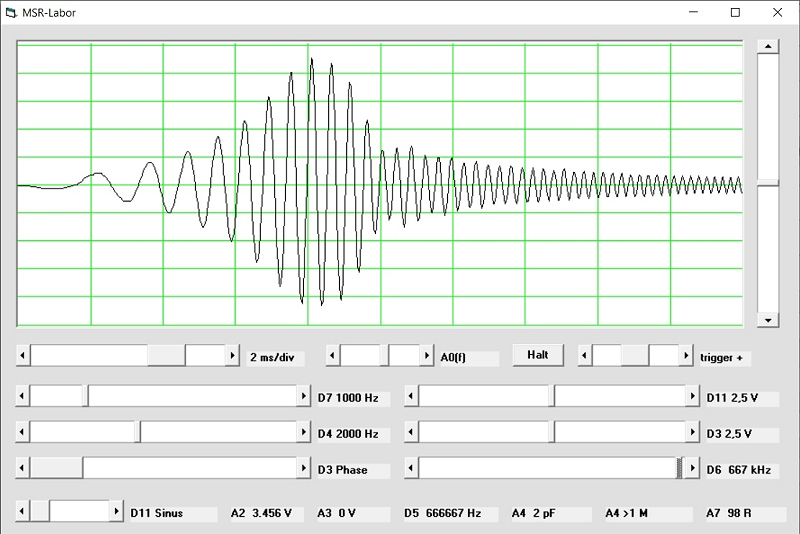
Kap 3.5 aus dem Arduino-Messlabor: Hier wird eine Lösung vorgestellt, die noch allein mit der Arduino-IDE und dem integrierten seriellen Plotter auskommt. Für den Anfang ist der serielle Plotter sehr bequem, weil man damit nicht an zwei Baustellen gleichzeig arbeiten muss. Als Zwischenlösung bietet es sich an, die Daten zuerst in einem Array zu speichern und dann erst abzusenden.
#include <math.h>
unsigned char dds[256];
unsigned char osz[500];
unsigned int ph, n, i, j;
ISR (TIMER0_OVF_vect)
{
PORTD |= 4;
ph += 256;
OCR0A = dds[ph >> 8];
if (i < 500) {
osz[i] = ADCH;
i++;
}
PORTD &= ~4;
}
int main(void)
{
unsigned int n;
Serial.begin(1000000);
for (n = 0; n < 256;
n++) dds[n] = 127 + 127 * sin(PI * n / 128.0);
DDRD = 254;
TCCR0A = 0xA3; //Timer0
Fast PWM an PD5/6
TCCR0B = 0x01; //16 MHz
TIMSK0 = 0x01; //Timer0
Overflow Interrupt
OCR0A = 128;
OCR0B = 128;
ADMUX = 0x60; //ADC Ref =
VCC, Left adjusted;
ADCSRB = 4; //4
'Timer0 Start 0= free running
ADCSRA = 0xE4; //ADC Enable,
Start, Auto Trigger, 1MHz;
sei();
while (true) {
i = 0;
for (n = 1; n < 65000;
n++) {
for (j = 1; j < 20;
j++){ asm ("nop");}
}
for (n = 0; n < 500;
n++) {
Serial.println(osz[n]);
}
}
}
Die Speicherung wird gestartet, wenn i von außen auf 0 gesetzt wird und beendet, wenn 0 = 499 erreicht wird. Die Ausgabe der 500 Messwerte erfolgt im Hauptprogramm. Zusätzlich wurde eine Warteschleife eingefügt, damit das Oszillogramm nach jeder Ausgabe für rund eine Sekunde still steht.
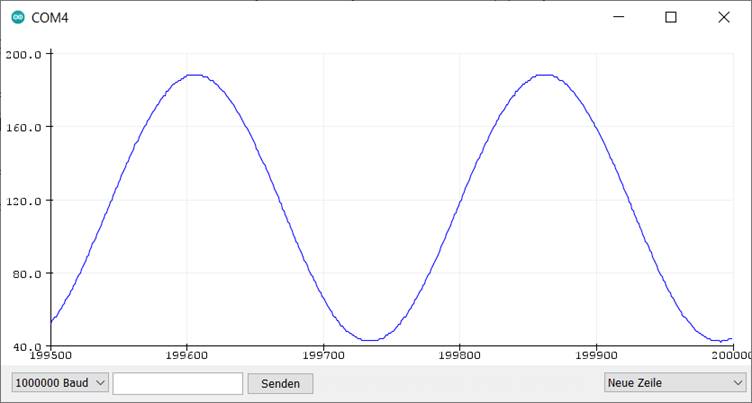
Eigenmessung des Sinussignals
Eine volle Sinusschwingung wird hier in 256 Punkten ausgegeben, sodass auf den Schirm mit seinen 500 Messpunkten fast zwei volle Schwingungen passen. Die Frequenz des Signals beträgt 244 Hz, wie oben im Zusammenhang mit Sägezahnsignalen schon berechnet wurde: 16 MHz / 256 / 256 = 244 Hz.

Externe Messung: 244 Hz, 2,5 Vss
Die Messung mit dem externen Oszilloskop bestätigt die Frequenz von 244 Hz. Das Sinussignal wird durchgehend erzeugt und zeigt keinerlei Unterbrechungen, Phasensprünge oder Verzerrungen durch die Messung. Während der seriellen Ausgabe der Daten kann die Ausgabe zwar durch den Timer-Interrupt unterbrochen werden, aber dies stört den Ablauf nicht.
Ein Blick auf das Signal an PD2 zeigt die geringe Auslastung der Interrupt-Routine von nur rund 10% der verfügbaren 16 µs.
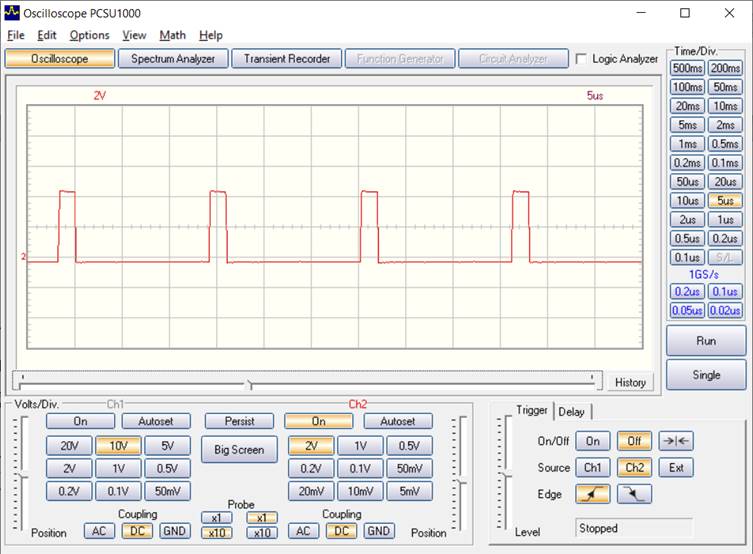
Messung der Zeitauslastung an D2
Das Programm lässt nun auch höhere Signalfrequenzen zu. Bei einer Sinusfrequenz von 2 kHz (ph += 2098;) erkennt man bereits Reste der PWM-Frequenz. Dass diese Reste an den Extremwerten der Sinusschwingung liegen, weist auf eine Phasenverschiebung von ca. 90 Grad hin. Das bedeutet zugleich dass das Tiefpassfilter schon weit jenseits seiner Grenzfrequenz von 160 Hz betrieben wird und dass die Amplitude des Nutzsignals mit 200 mV dementsprechend gering wird. Das grundlegende Problem ist, dass die PWM-Frequenz möglichst weit oberhalb der Nutzfrequenz liegen sollte, sie aber bei einer Auflösung von 8 Bit auf 62,5 kHz begrenzt ist. Eine mögliche Lösung liegt in einem mehrpoligen Tiefpassfilter mit größerer Flankensteilheit. Dieses Thema wird weiter unten noch genauer behandelt.
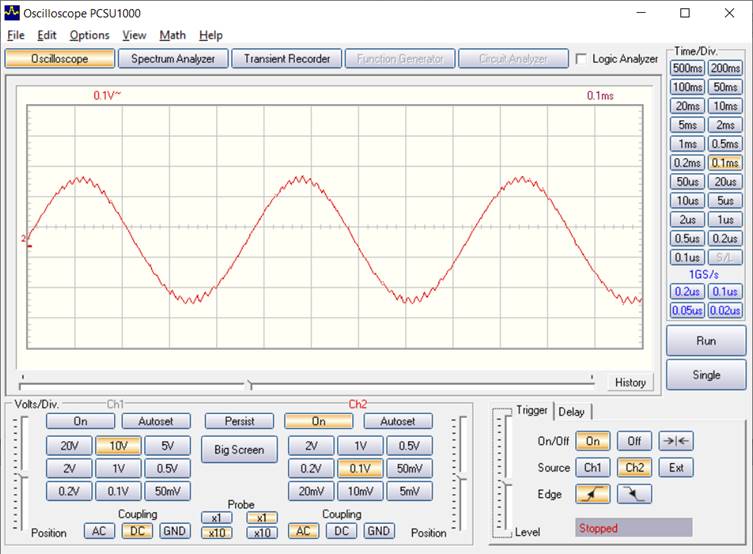
Das erzeugte 2-kHz-Signal über 10 kΩ an 100 nF
Die Eigenmessung mit dem Arduino-Plotter zeigt, dass ein Signal von 2 kHz schon sehr gut dargestellt wird. Für diese Messung wurde die Grenzfrequenz des Tiefpassfilters auf 1,6 kHz erhöht (10 kΩ und 10 nF), damit die Signalspannung besser zum Messbereich 5 V passt. Reste des PWM-Signal sind hier nicht zu entdecken. Das liegt aber daran, dass die AD-Abtastung synchron zum PWM-Signal erfolgt. Ein noch vorhandenes Restsignal mit 62,5 kHz würde immer in derselben Phase gemessen und damit als glatt erscheinen. Man muss also im Hinterkopf behalten, dass die synchrone Messung das Signal etwas perfekter darstellt, als es tatsächlich ist. Die Vergleichsmessung mit einem externen Oszilloskop und höherer Abtastrate zeigt unter den gleichen Bedingungen (2 kHz, 10 kΩ und 10 nF) dagegen noch Reste des PWM.
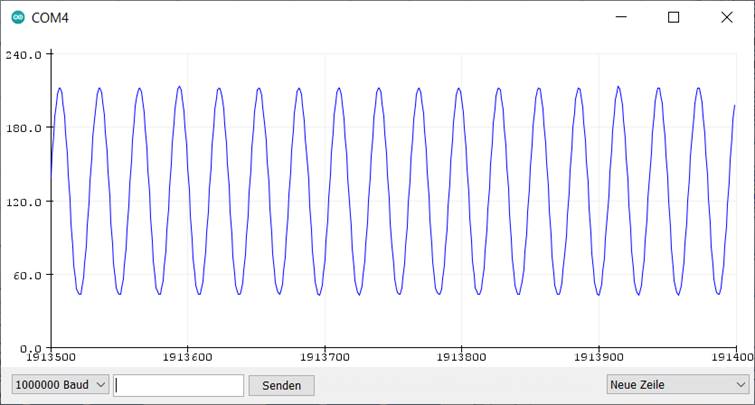
Messung des eigenen 2-kHz-Signales über 10 kΩ an 10 nF
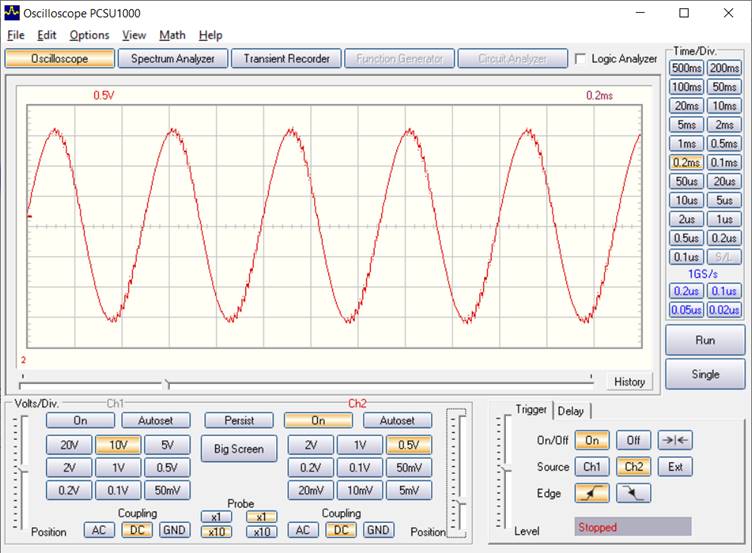
Vergleichsmessung mit einem externen Oszilloskop
Das Oszilloskop ist mit seiner Abtastrate von 62,5 kHz bereits voll tauglich für den gesamten NF-Bereich. Entscheidend ist ja, dass die Abtastrate mindestens doppelt so hoch liegt wie die höchste vorkommende Signalfrequenz. Im Audiobereich verwendet man oft eine Abtastrate von 44,1 kHz für den Frequenzbereich bis 20 kHz, wobei allerdings sehr steilflankige Filter eingesetzt werden. Die Abtastrate liegt also höher als erforderlich. Daher kann auch das mit dem Arduino realisierte Oszilloskop schon typische Audiosignale korrekt darstellen.
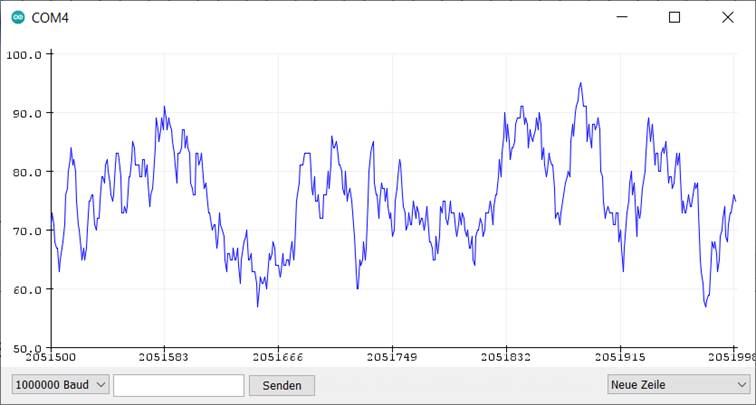
Darstellung eines Musiksignals aus dem Radio
#include <math.h>
unsigned char dds[256];
unsigned char osz[500];
unsigned int ph, n, i, j;
ISR (TIMER0_OVF_vect)
{
PORTD |= (1 << PD2);
//ph += 256;
ph += 512;
//ph += 2098;
OCR0A = dds[ph >> 8];
OCR0B = OCR0A;
if (i < 500) {
osz[i] = ADCH;
i++;
}
PORTD &= ~(1 << PD2);
}
int main(void)
{
unsigned int n;
Serial.begin(1000000);
for (n = 0; n < 256; n++) dds[n] = 127 + 127 * sin(PI * n / 128.0);
DDRD |= (1 << PD2) | (1 << PD5) | (1 << PD6); // OC0B, OC0A
TCCR0A = (0b10 << COM0A0) | (0b10 << COM0B0) | (0b11 << WGM00); //0xA3; //Timer0 Fast PWM an PD5/6
TCCR0B = (0b001 << CS00); //16 MHz
TIMSK0 = (1 << TOIE0); // 0x01; //Timer0 Overflow Interrupt
OCR0A = 128;
OCR0B = 128;
ADMUX = (0b01 << REFS0) | (1 << ADLAR); //0x60; //ADC Ref = VCC, Left adjusted;
ADCSRB = (0b100 << ADTS0); // 4; //4 'Timer0 Start 0= free running
ADCSRA = (1 << ADEN) | (1 << ADSC) | (1 << ADATE) | (0b100 << ADPS0); // 0xE4; //ADC Enable, Start, Auto Trigger, 1MHz;
sei();
while (true) {
i = 0;
for (n = 1; n < 65000; n++) {
for (j = 1; j < 20; j++){ asm ("nop");}
}
for (n = 0; n < 500; n++) {
Serial.println(osz[n]);
}
}
}