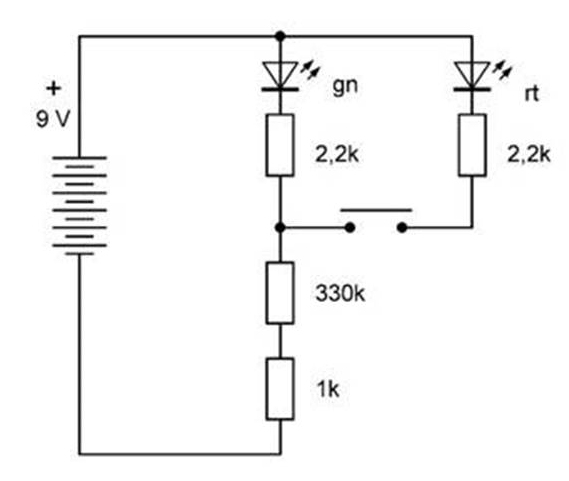
2.4 Farbumschalter

von Andreas Thaler

Elektronik-Labor Projekte Lernpakete Grundschaltungen

In dieser Schaltung von Burkhard Kainka sind zwei LEDs parallelgeschaltet und über eine gemeinsame Strecke mit Masse verbunden. Ein Schalter trennt die rote LED von der Masseverbindung ab.

Bei offenem Schalter fließt Strom über die grüne LED, die in Reihe mit dem 2,2 kOhm-, 330 kOhm- und 1 kOhm-Wiederstand geschaltet ist. Der Ersatzwiderstand für die drei Widerstände beträgt 333,2 kOhm (Addition der drei Widerstandswerte). Aufgrund des hohen Ersatzwiderstandes ist davon auszugehen, dass die grüne LED kaum oder nicht leuchten wird. Da die rote LED bei offenem Schalter nicht mit Masse verbunden ist, fließt durch sie und den zweiten 2,2-kOhm-Widerstand kein Strom.

Bei geschlossenem Schalter fließt Strom durch beide LEDs über die gemeinsame Strecke nach Masse. Für beide LEDs beträgt der Ersatzwiderstand 333,2 kOhm, wobei die rote LED den ersten 2,2-kOhm-Widerstand überbrückt. Aufgrund der Parallelschaltung beider LEDs mit einem gemeinsamen Ausgang nach Masse teilt sich der Strom auf. Da die Vorwärtsspannung der roten LED etwas niedriger ist als die der grünen LED (angenommene 1,8 Volt gegenüber 2,0 Volt), ist ihr Widerstand etwas geringer. Deshalb fließt durch die rote LED mehr Strom als durch die grüne. Auch für die rote LED ist aufgrund des hohen Ersatzwiderstandes davon auszugehen, dass sie nur etwas heller als die grüne LED leuchtet, wenn überhaupt.

Jede LED bildet mit den nachgeschalteten Widerständen eine Reihenschaltung. Entsprechend fällt die Eingangsspannung jeweils an den LEDs und Widerständen ab, wobei der größte Spannungsabfall am 330-kOhm-Widerstand (höchster Widerstandwert in der Reihenschaltung) auftritt.

Berechnung der Gesamtströme

Bevor wir diese Schaltung simulieren, berechnen wir die Gesamtströme so gut als möglich. Wir können dann bereits eine Aussage darüber treffen, ob die LEDs ausreichend Strom zum Leuchten erhalten.

Wie aus den vorangegangenen Experimenten bekannt, lässt sich der Spannungsabfall an einer LED nur schwer vorhersagen. Wir gehen daher von Standardwerten aus, das sind 2,0 Volt Vorwärtsspannung bei der grünen und 1,8 Volt Vorwärtsspannung bei der roten LED. Da wir in der Schaltung einen hohen Ersatzwiderstand haben, an dem eine entsprechend hohe Teilspannung abfällt, schätzen wir den Spannungsabfall an den beiden LEDs mit 1,7 Volt für die grüne und 1,63 Volt für die rote LED. Da bislang keine Erfahrungswerte vorliegen, wird das Ergebnis vermutlich mehr oder weniger von den tatsächlich gemessenen Spannungsabfällen abweichen.

Für die beiden LEDs fertigen wir jeweils ein Ersatzschaltbild mit dem Ersatzwiderstand an:

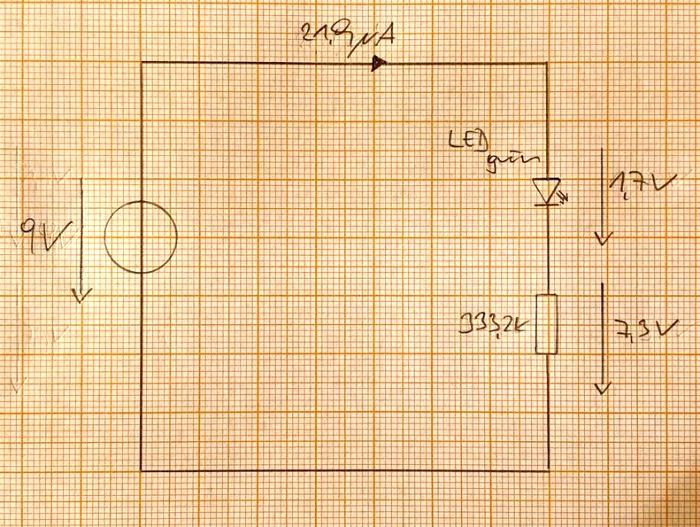
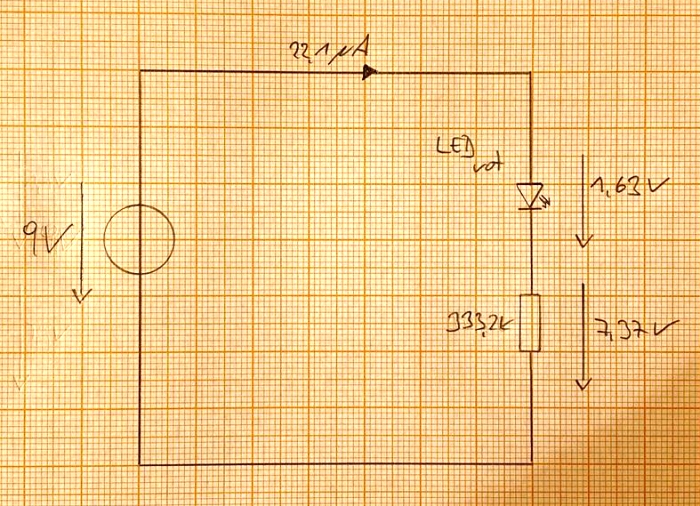
Gesamtströme

U_E = 9 V
R_Ersatz = 333,2 kOhm
U_{LED grün} ~ 1,7 V
U_{LED rot} ~ 1,63 V

I_{ges
LED grün:}

U = R * I
I = U/R

7,3 V = 333,2 kOhm * I
I = 7,3 * 10⁰V/ 333,2 * 10³ Ohm
I = (7,3 / 333,2) * 10^-3 A
I = 0,0219 mA
I_{ges
LED grün}= 21,9 uA

I_{ges
LED rot:}

U = R * I
I = U/R

7,37 V = 333,2 kOhm * I
I = 7,37 * 10⁰V/ 333,2 * 10³ Ohm
I = (7,37 / 333,2) * 10^-3 A
I = 0,0221 mA
I_{ges
LED rot}= 22,1 uA

Gemessen am Standardwert von 20 mA für den Betrieb einer LED wird bei diesen Stromstärken im Mikroampere-Bereich mit nur wenig Leuchten zu rechnen sein.

Simulation der Schaltung in EveryCircuit

Wir bauen die Schaltung wieder in der Schaltungssimulation EveryCircuit auf.

Zuerst mit dem errechneten Ersatzwiderstand von 333,2 kOhm und dann mit den tatsächlichen Einzelwiderständen. In beiden Varianten müssen die Gesamtströme ident sein.

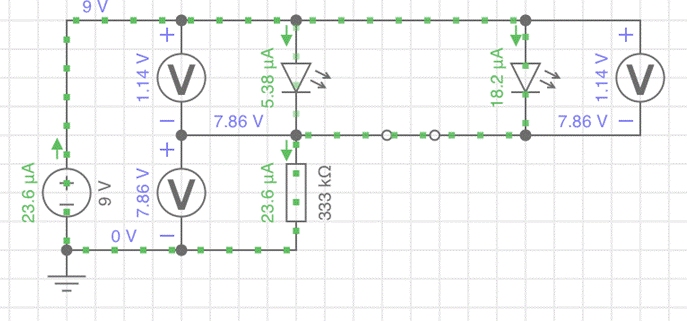
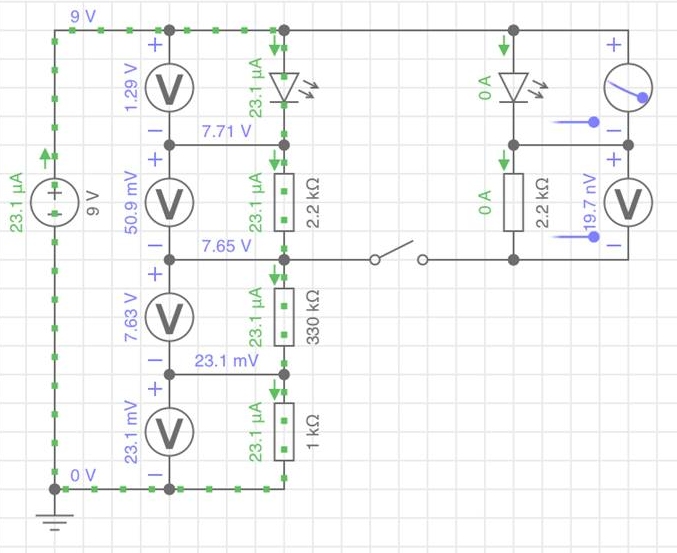
Die Gesamtströme stimmen in beiden Simulationsvarianten überein. Das heißt, die Annahme eines Ersatzwiderstandes, der Einzelwiderstandswerte zusammenfasst, ist verifiziert. Wie sieht es nun mit der Gegenüberstellung unserer berechneten Werte zu den Werten in der Simulation aus? Sehr ermutigend: für die grüne LED 21,9 uA zu 23,1 uA und für die rote LED 22,1 uA zu 23,6 uA.

Aber halt! In der Simulation sehen wir doch, dass für die rote LED der Gesamtstrom zwar 23,6 uA beträgt aber effektiv fließen durch die rote LED nur 17,2 uA? Der Grund dafür liegt darin, dass die grüne LED noch genügend Spannung erhält, um Strom durchzulassen. Und das tut sie und schnappt der roten LED die Differenz auf den Gesamtstrom in Höhe von 6,43 uA weg. Würden wir die grüne LED von der Stromversorgung trennen, erhielte die rote LED den Gesamtstrom und leuchtete heller.

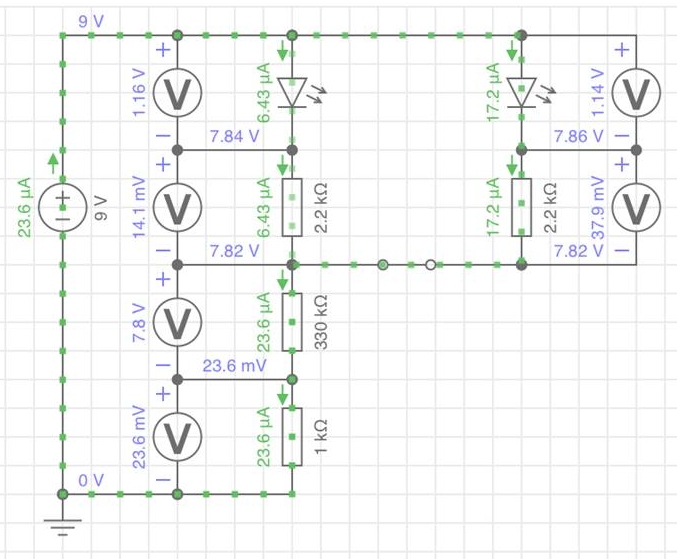
Haben Sie es bemerkt? In der Ersatzschaltung fließt etwas mehr Strom durch die rote LED als in der Schaltung mit Einzelwiederständen. Das liegt daran, dass in der Schaltungssimulation statt 333,2 nur 333 Ohm eingegeben werden können. Damit ist der Widerstand geringfügig kleiner und es fließt mehr Strom. Sehen wir uns nun an, ob sich das alles auch an der realen Schaltung bestätigen lässt.

Aufbau der Schaltung am Steckbrett

Schaltung mit anliegender Eingangsspannung in der Höhe von 9 Volt (stabilisiertes Labornetzgerät) und offenem Schalter. Die rote LED leuchtet nicht.

Schaltung mit geschlossenem Schalter. Die grüne LED leuchtet nicht, die rote schwach (auf dem Foto nicht zu erkennen).

Messwerte

	Schalter offen (V)	Schalter geschlossen (V)
U_{LED grün}	1,68	1,62
U_{LED rot}	0	1,60
U_{R 2,2 k (1)}	0,047	0,016
U_{R 2,2 k (2)}	0	0,032
U_{R 330k}	7,24	7,34
U_{R 1k}	0,021	0,022

Werte Simulation

	Schalter offen (V)	Schalter geschlossen (V)
U_{LED grün}	1,29	1,16
U_{LED rot}	0	1,14
U_{R 2,2 k (1)}	0,051	0,014
U_{R 2,2 k (2)}	0	0,038
U_{R 330k}	7,63	7,80
U_{R 1k}	0,023	0,024

Fazit

Messwerte und Simulation stimmen hinsichtlich der Gesamtströme gut überein.

Differenzen gibt es bei den Spannungsabfällen an LEDs und dem größten Widerstand mit 330 kOhm. Das kann daran liegen, dass die Simulation den LED-Widerstand anders bewertet als er tatsächlich ist. Oder die realen LEDs weichen von der angenommenen Vorwärtsspannung von 2,0 Volt für grün und 1,8 Volt für rot ab.

Schauen wir, was Burkhard Kainka dazu meint :-)

(Anmerkungen BK: Bei den ersten LEDs konnte man sich noch darauf verlassen, dass die Durchlassspannung proportional zur Frequenz des Lichts war. Ansonsten entsprach die Kennlinie fast genau der einer Si-Diode, nur eben zu höheren Spannungen verschoben. In den letzten Jahrzehnten sind die LEDs immer besser geworden, was den Wirkungsgrad angeht, und immer kreativer, was die Kennlinie angeht. Die roten LEDs brauchen jetzt deutlich mehr Spannung und sind näher an die grünen gerückt. Außerdem ist der Bahnwiderstand größer geworden und wirkt wie ein zusätzlicher Vorwiderstand, was wohl erwünscht war, damit man LEDs ohne Vorwiderstand einsetzen kann. Bei einer genauen Messung an einer superhellen grünen LED ist mir aufgefallen, dass die Kennlinie so aussieht, als wären zwei Dioden in Reihe geschaltet. Die LED-Hersteller greifen immer tiefer in die Trickkiste der Quantenphysik, und der Fortschritt ist nicht aufzuhalten. Aber das bedeutet auch, dass man das genaue Verhalten einer LED immer schwerer voraussagen kann. Was mit alten LEDs eindeutig war, kann mit den modernsten LEDs ganz anders aussehen. Und weil der Wirkungsgrad so gut geworden ist, kommt man mit viel kleineren Strömen aus. Manch ein Arduino hat immer noch dieselben Vorwiderstände wie vor zehn Jahren, aber die LEDs sind jetzt blendend hell, so hell, dass es in den Augen weht tut und man ausschalten muss, um die Beschriftung der Anschlüsse genau zu erkennen.)

Für unsere Praxis sind selbst diese größeren Abweichungen unerheblich. Die Berechnung des Gesamtstromes (auf Basis Schätzung des Spannungsabfalls an beiden LEDs), die Simulation und der tatsächliche Wert liegen eng beinander. Wir haben gesehen, dass der Gesamtstrom in jedem Fall für die grüne LED zu wenig ist und für die rote LED gerade ausreichend, um sie etwas zum Leuchten zu bringen. Wir können in der realen Schaltung dann immer noch mit Anpassung der Widerstände nachjustieren.

Viel wichtiger als die Abweichung der Werte ist das Verständnis der Schaltung. Der Strom bevorzugt den Weg des geringeren Widerstandes, das konnten wir demonstrieren. Oder anders gesagt: Der Strom verteilt sich je nach Verhältnis der Widerstände in einer Parallelschaltung. Wo weniger Widerstand ist, fließt er reichlicher, aber so gut wie nie ausschließlich.

^{http://www.elektronik-labor.de/Lernpakete/Schaltung/Grundschaltungen2_2.html}

^{http://www.elektronik-labor.de/Lernpakete/Schaltung/Grundschaltungen2_1.html}